Let ![]() be a separated scheme over
be a separated scheme over ![]() .
That means, we are given a separated morphism
.
That means, we are given a separated morphism
![]() .
Let
.
Let
![]() be the defining ideal sheaf of
the diagonal
be the defining ideal sheaf of
the diagonal ![]() in
in
![]() .
For any positive integer
.
For any positive integer ![]() , we define
, we define
![]() to be
the closed subscheme of
to be
the closed subscheme of
![]() defined by
defined by
![]() .
.
The sheaf
![]() on
on ![]() is called the sheaf of
is called the sheaf of
![]() -jets on
-jets on ![]() relative to
relative to ![]() .
There is another description of this sheaf.
Let
.
There is another description of this sheaf.
Let
be restrictions of the projections
For a local section ![]() of
of
![]() , we define the jet
(``the Taylor expansion'') of
, we define the jet
(``the Taylor expansion'') of ![]() (of order
(of order ![]() ) by
) by
Then we have
![]() . The sheaf of
. The sheaf of ![]() -jets on
-jets on ![]() relative to
relative to ![]() is
is
Let us put

When ![]() is not invertible in
is not invertible in ![]() , a similar formula is still valid.
The thing is that the operator
, a similar formula is still valid.
The thing is that the operator
![]() is defined over
is defined over
![]() .
.
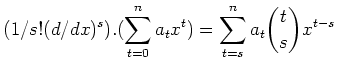
Like wise, for any quasi coherent sheaf
![]() on
on ![]() , we may define
the sheaf
, we may define
the sheaf
![]() of
of ![]() -jets of
-jets of
![]() on
on ![]() relative to
relative to ![]() as
as
For any local section