


Next: The sheaf of differential
Up: Linear differential operators
Previous: definition of linear differential
Differential operators are defined locally. Thus we may restrict ourselves
to the affine case and look them carefully by the language of algebras and
modules.
PROOF..
In
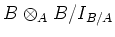
, every class
![$ [\sum_j f_j\otimes g_j]$](img300.png)
of an element
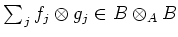
is equal to
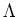
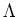
Using the Lemma of criterion for being a differential operator,
We deduce the following useful lemma.
COROLLARY 9.13
A composition of an 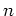 -th order differential operator
-th order differential operator
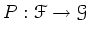 and an
and an 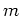 -th order differential operator
-th order differential operator
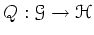 is
a differential operator of
is
a differential operator of 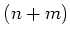 -th
order.
-th
order.
PROOF..
We note that for any local regular function
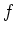
, w
holds.
Then we may easily verify the statement by using induction.
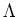
DEFINITION 9.14
For any separable scheme
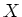
over
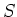
, we denote the sheaf of
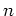
-th
linear differential operators on
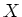
from a quasi coherent sheaf
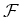
to a quasi coherent sheaf
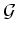
relative to
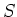
by
The inductive limit
is called the sheaf of
linear differential operators on
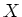
relative to
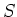
.
We use the following abbreviational symbols.
Note that
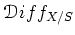 is a sheaf of algebras over
is a sheaf of algebras over 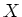 .
It is an important example of an object which is
a ``non-commutative algebras glued together''.
.
It is an important example of an object which is
a ``non-commutative algebras glued together''.
ARRAY(0x9f21498)ARRAY(0x9f21498)ARRAY(0x9f21498)



Next: The sheaf of differential
Up: Linear differential operators
Previous: definition of linear differential
2011-03-03
![$\displaystyle [\sum_j f_j\otimes g_j]
=
\sum_j [f_j\otimes 1] [1\otimes g_j]
=
\sum_j [1\otimes f_j] [1\otimes g_j]
= [1\otimes \sum_j f_j g_j]
$](img302.png)
![]()
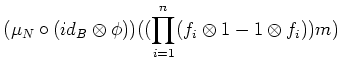
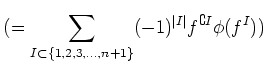
![]()
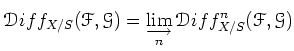
![]() is a sheaf of algebras over
is a sheaf of algebras over ![]() .
It is an important example of an object which is
a ``non-commutative algebras glued together''.
.
It is an important example of an object which is
a ``non-commutative algebras glued together''.