|
( |
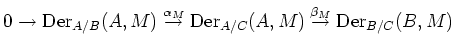 |
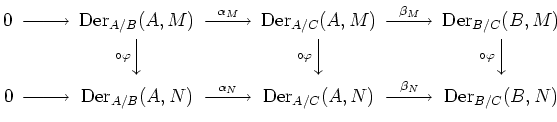 |
Any ![]() -derivation
-derivation ![]() over
over ![]() defines by restriction a
defines by restriction a ![]() -derivation
-derivation ![]() over
over ![]() which
we denote by
which
we denote by
![]() .
.
The rest is easy observation.
![]()
With the help of universality of ![]() , we obtain the following corollary.
, we obtain the following corollary.
|
( |
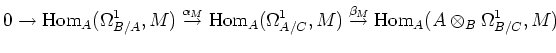 |
ARRAY(0x9f219e8)
We assume that the assignment
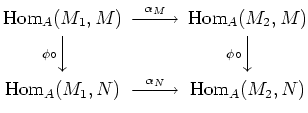
In other words, we have
for any
holds for all
We assume that the assignments
![]() is natural.
Assume furthermore that for any
is natural.
Assume furthermore that for any ![]() -module
-module ![]() , a sequence
, a sequence
|
( |
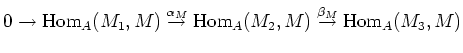 |
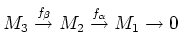
(which arises due to the claim above) is also exact.
Then for any
(2) Since
![]() ,
we deduce that
,
we deduce that
![]() using the uniqueness of the
homomorphism which represents
using the uniqueness of the
homomorphism which represents
![]() .
.
For surjectivity of ![]() , we use the sequence
, we use the sequence ![]() for
for
![]() .
For the exactness at the middle term,
we use the sequence
.
For the exactness at the middle term,
we use the sequence ![]() for
for
![]() .
We leave the detail as an easy exercise.
.
We leave the detail as an easy exercise.
![]()