PROOF..
Let us denote by
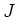
the ideal of
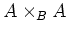
generated by
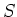
.
Then we define a subset
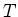
of
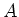
as follows.
Now we claim the following facts.
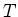 is closed under addition.
is closed under addition.
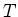 is stable under multiplication by any element of
is stable under multiplication by any element of 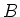 .
.
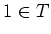 .
.
-
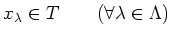 .
.
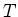 is closed under multiplication.
is closed under multiplication.
The only (5) may require proof. For any elements
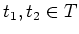
, we have
So the subset 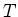 is a
is a 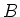 -subalgebra of
-subalgebra of 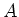 containing the generators
containing the generators
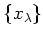 of
of 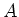 . Thus we have
. Thus we have 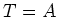 .
.
PROOF..
Let us first prove the ``if'' part. Assume
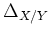
is open.
then
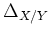
is a clopen (``closed and open'') subset of
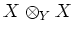
.
Namely,
is a decomposition of the scheme
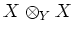
into two Zariski open set.
Thus we have
We then note in particular that
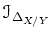
has
a distinguished global section (``the identity'')
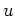
defined by
Then we see that
So we have
as required.
Let us now prove the ``only if'' part. The question is local on 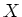 and on
and on 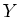 .
So we may assume that
.
So we may assume that 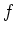 is of the form
is of the form
where
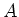
is a finitely generated algebra over
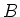
.
Let
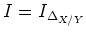
be the ideal of definition of the diagonal.
The previous Lemma tells us that
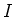
is finitely generated over
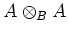
.
By the assumption we have
Now we use the Nakayama's lemma (theorem below) to find an element
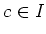
such that
Then it is easy to see that
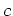
is an idempotent and that
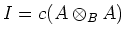
is its range.
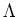
![]() is a
is a ![]() -subalgebra of
-subalgebra of ![]() containing the generators
containing the generators
![]() of
of ![]() . Thus we have
. Thus we have ![]() .
.
![]()
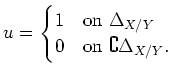
![]() and on
and on ![]() .
So we may assume that
.
So we may assume that ![]() is of the form
is of the form