


Next: appendix
Up: Étale morphism
Previous: Étale morphism
For any non negative integer 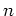 and for any scheme
and for any scheme 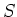 , we put
, we put
and
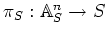 the standard projection.
the standard projection.
A smooth scheme over 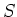 is a scheme which ''étale locally look like''
is a scheme which ''étale locally look like''
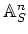 .
.
DEFINITION 10.7
A separated morphism
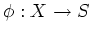
of finite type
is smooth of relative dimension
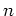
if for any point
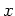
on
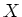
, there exists
an open neighborhood
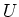
of
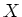
and an 'etale morphism
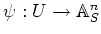
such that
holds.
Let us close this section by quoting the following fundamental result.
2011-03-03
![]() and for any scheme
and for any scheme ![]() , we put
, we put
![]() is a scheme which ''étale locally look like''
is a scheme which ''étale locally look like''
![]() .
.