- If
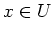 and
and 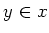 , then
, then 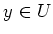 .
.
- If
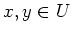 , then
, then
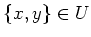 .
.
- If
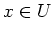 , then the power set
, then the power set 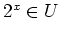 .
.
- If
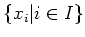 is a family of elements of
is a family of elements of
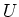 indexed by an element
indexed by an element 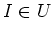 ,
then
,
then
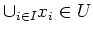 .
.
In this text we always assume the following.
For any set ![]() , there always exists a universe
, there always exists a universe ![]() such that
such that ![]() .
.
The assumption above is related to a ``hard part'' of set theory. So we refrain ourselves from arguing the ``validity" of it.
Note: The treatment in this subsection owes very much on those of wikipedia:
http://en.wikipedia.org/wiki/Small_set_(category_theory)and planetmath.org:
http://planetmath.org/encyclopedia/Small.htmlbut the treatment here differs a bit from the treatments given there. We also refer to [13] as a good reference.