Secondly, we add a notation.
DEFINITION 5.8
Let
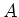
be a commutative ring. Let
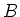
be a commutative
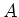
-algebra.
Let
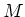
be a
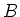
-module with a connection
Then for any
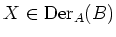
,
is an
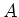
-linear map. We shall denote it by
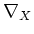
.
PROOF..
Let
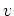
be an element of
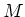
.
Since
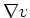
is an element of
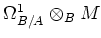
, we may
write it as :
for some
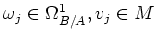
.
Then we compute
On the other hand, we have
So we may proceed
Thus, together with the Lemma above, we see
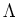
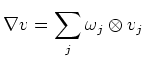
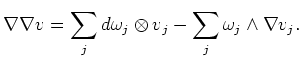
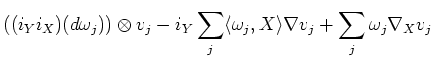
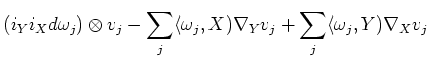
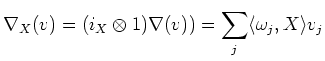
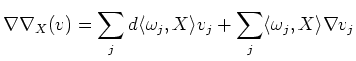
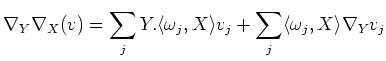
![$\displaystyle i_Y i_X \nabla \nabla (v)+ \nabla_Y \nabla_X(v)-\nabla_X\nabla_Y(v)
=-\sum_j i_{[X,Y]}\omega_j \otimes v_j=-\nabla_{[X,Y]} v
$](img214.png)
![]()