- Let
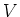 be a finite dimensional representation of
be a finite dimensional representation of  . Let
. Let 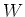 be a subrepresentation of
be a subrepresentation of 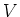 . Then we have
. Then we have
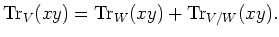
- Let
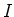 be an ideal of
be an ideal of  . Assume
. Assume  is finite dimensional. Then we have
is finite dimensional. Then we have
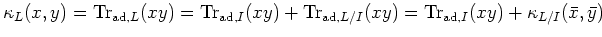
(where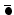 denotes the class of
denotes the class of 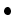 in
in 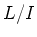 .)
In particular, for any
.)
In particular, for any 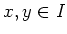 , we have
, we have
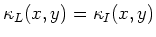
PROOF..
(2): We choose a basis
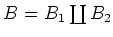 of
of  such that
such that 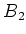 forms a
basis of
forms a
basis of 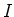 . Then
. Then 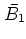 forms a basis of
forms a basis of 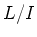 .
Under the basis
.
Under the basis 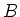 ,
,
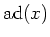 may be represented by a matrix
may be represented by a matrix
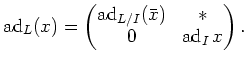
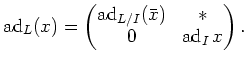
We obtain the result easily from this.
(1): may be proved in a same manner.
![]()