

Next: Cartan's criterion for semisimplicity
Up: generalities in finite dimensional
Previous: Theorem of Iwasawa
Cartan's criterion relates several properties (semi simplicity, solvability)
of Lie algebras with properties of their invariant bilinear forms.
To prove it we need some study on bilinear forms.
DEFINITION 5.32 (in this subsection only)
For any free module
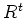
over a ring
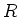
,
We denote by
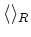
the ``usual inner product''. That is,
The first thing we do is to observe the property of this inner product
when the base ring 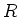 is a ``real field''. (Since we only need it for the
case
is a ``real field''. (Since we only need it for the
case
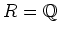 , we omit the definition of a real field and describe the
following lemma only when
, we omit the definition of a real field and describe the
following lemma only when
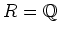 .)
.)
PROOF..
Assume
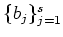
are linearly dependent over
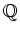
.
Then there exists a non trivial vector
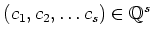
such
that
holds. Thus
So
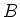
is a degenerate matrix which implies that
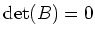
.
Let us now prove the opposite implication.
Assume 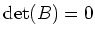 .
Then there exists a non trivial vector
.
Then there exists a non trivial vector
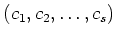 such that
such that
holds. Let us put
Then we see that
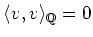
and hence
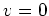
.
(Note that for this implication we have used the fact
that
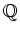
is a ``real field''.)
Thus
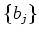
are linearly dependent over
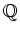
.
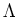
The next task is to compare
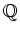 with other field.
with other field.
DEFINITION 5.34
For any subset
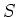
of a
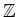
-module
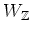
,
Let us put
(``The maximum modulus of Gram determinants''.)
We denote by
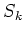
the subset of
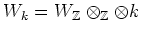
defined by
LEMMA 5.35
Let 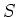 be a finite subset of a free module
be a finite subset of a free module
over
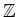 .
Let
.
Let 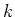 be a field of characteristic
be a field of characteristic 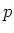 .
We assume either
.
We assume either 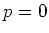 or
or
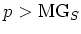 holds.
Then we have
holds.
Then we have
PROOF..
Assume
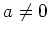
. Since the inner product
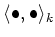
is non degenerate on
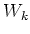
, we see that
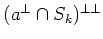
is equal to the
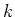
-vector space spanned by
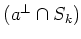
.
Thus there exists a set of
linearly independent vectors
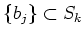
so that we may write down
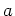
as
Then by the assumption on
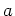
, we see that
Thus
which is equivalent to
|
(1) |
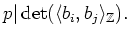 |
Note on the other hand that 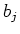 are linearly independent over
are linearly independent over
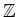 .
Thus
.
Thus
By the definition of
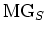
, we see that
|
(2) |
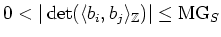 |
which contradicts to the condition (
1).
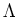
DEFINITION 5.36
For any positive integer
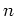
, and for any ring
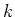
, we denote by
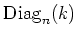
the set of diagonal matrices in
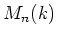
.
For any vector
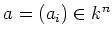
, we denote by
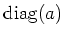
the diagonal matrix
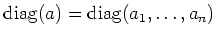
.
Note that for any ring
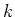
, the restriction of the Killing form of
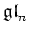
coincides with the ``usual'' inner product with this identification. That is,
We define the following subset of
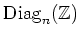
.
(where the vectors
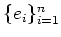
are elementary vectors.)
We note that an obvious estimate
holds.
PROOF..
Let us denote by
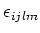
the vector
We first find a map
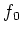
from
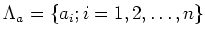
to
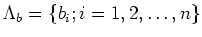
such that
Such a thing exists (is ``well defined'') if and only if
holds. This condition is equivalent to the condition
which holds by the assumption on
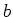
. Thus we see that
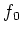
exists.
On the other hand,
by using Lagrange interpolation formula we see that there
exists a polynomial
![$ f\in k[X]$](img495.png)
such that
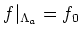
.
Then we have
The adjoint action of a diagonal matrix
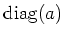 is
represented by a diagonal matrix
is
represented by a diagonal matrix
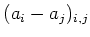 .
Thus an argument similar to the one above proves the existence of
.
Thus an argument similar to the one above proves the existence of 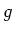 .
.
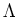
PROOF..
We may assume that
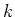
is algebraically closed.
Let us take an element
![$ x \in [L,L]$](img501.png)
.
Then we have
Let us now diagonalize
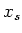
and write
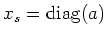
.
Let us take arbitrary
![$ b\in (a^\perp\cap S^{[n]})^\perp$](img484.png)
.
By the lemma above we see that there exist polynomials
![$ f,g\in k[X]$](img485.png)
such
that
holds.
For any
![$ w=\sum_l [y_l z_l]\in [L,L]$](img504.png)
, we have:
That means,
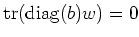
. In particular, we have
Since
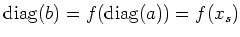
is a polynomial in
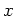
,
it commutes with
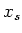
and with
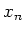
.
thus
gives the Jordan-Chevalley decomposition of
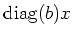
. Therefore,
thus
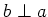
.
To sum up, we have shown
In other words,
which is equivalent to saying that
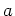
is a linear combination of
elements in
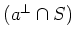
.
In view of Lemma 5.35, we see that 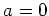 .
So
.
So
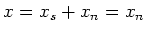 is a nilpotent element.
is a nilpotent element.
By the theorem of Engel, we conclude that ![$ [L,L]$](img521.png) is nilpotent.
Thus
is nilpotent.
Thus 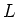 is solvable
(since we have shown that
is solvable
(since we have shown that ![$ L/[L,L]$](img522.png) and
and ![$ [L,L]$](img521.png) are solvable).
are solvable).
Note:
The estimate given in the above corollary is presumably far from the best one.
PROPOSITION 5.41
Let 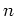 be a positive integer.
Let
be a positive integer.
Let 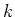 be a field of characteristic
be a field of characteristic
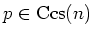 .
Let
.
Let 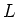 be a Lie algebra over
be a Lie algebra over 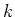 whose dimension is
less than or equal to
whose dimension is
less than or equal to 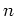 .
If the usual Killing form
.
If the usual Killing form
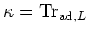 of
of 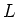 is identically equal to zero,
then
is identically equal to zero,
then 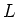 is solvable.
In particular, if
is solvable.
In particular, if 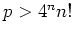 or
or 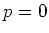 , then
, then 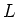 is solvable if its usual
Killing form is identically equal to zero.
is solvable if its usual
Killing form is identically equal to zero.
PROOF..
Apply the definition to
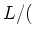
center of


Next: Cartan's criterion for semisimplicity
Up: generalities in finite dimensional
Previous: Theorem of Iwasawa
2009-03-06
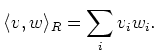
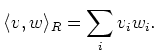
![]() is a ``real field''. (Since we only need it for the
case
is a ``real field''. (Since we only need it for the
case
![]() , we omit the definition of a real field and describe the
following lemma only when
, we omit the definition of a real field and describe the
following lemma only when
![]() .)
.)
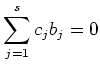
![]() .
Then there exists a non trivial vector
.
Then there exists a non trivial vector
![]() such that
such that
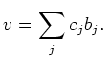
![]() with other field.
with other field.
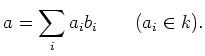
![]() are linearly independent over
are linearly independent over
![]() .
Thus
.
Thus
![]() satisfies
satisfies
![]() ,
then there exist polynomials
,
then there exist polynomials
![]() such that
such that
![]() is
represented by a diagonal matrix
is
represented by a diagonal matrix
![]() .
Thus an argument similar to the one above proves the existence of
.
Thus an argument similar to the one above proves the existence of ![]() .
.
![]()
![$\displaystyle \operatorname{tr}(\operatorname{diag}(b)[\sum_l y_l z_l]) =\sum_l\operatorname{tr}([\operatorname{diag}(b),y_l] z_l)$](img505.png)
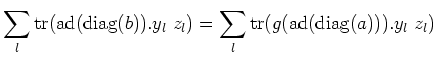
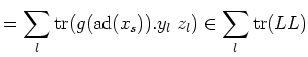
![]() .
So
.
So
![]() is a nilpotent element.
is a nilpotent element.
![]() is nilpotent.
Thus
is nilpotent.
Thus ![]() is solvable
(since we have shown that
is solvable
(since we have shown that ![]() and
and ![]() are solvable).
are solvable).
![]()
![]() associated to
associated to ![]() is identically zero,
is identically zero, ![]() is solvable.
is solvable.
![]() be a positive integer. We denote by
be a positive integer. We denote by
![]() the set of
the set of ![]() such
that Ccs holds for any Lie algebra
such
that Ccs holds for any Lie algebra ![]() of dimension less than or equal
to
of dimension less than or equal
to ![]() for any field
for any field ![]() of characteristic
of characteristic ![]() .
.