


Next: Semi direct products of
Up: generalities in finite dimensional
Previous: examples
DEFINITION 5.47
Let

be a finite dimensional Lie algebra.
Let
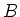
be a non-degenerate invariant bilinear form on

.
Then we define the
Casimir element
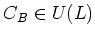
with respect to
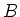
by
where
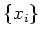
is a basis of

, and
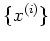
is the dual basis of
the basis
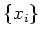
with respect to
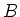
.
PROOF..
(1): easy exercise in linear algebra.
(2):
For any 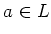 , let us write the adjoint action of
, let us write the adjoint action of 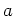 on
on  by using
the basis
by using
the basis 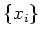 . Namely,
. Namely,
Then the constants
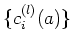
(``structure constants'')
are expressed in terms of
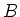
as follows.
We note that from the invariance of
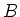
, we have
so that we have a dual expression
Then we compute as follows.
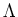
DEFINITION 5.49
Let

be a finite dimensional Lie algebra.
Let
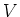
be a finite dimensional

-module.
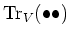
with respect to
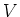
.
We assume that the Killing form
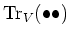
with respect to
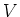
is non degenerate.
Then we define the
Casimir element with respect to
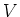
by
We see immediately from the definition that
holds in general.
LEMMA 5.50
Let  be a field of characteristic
be a field of characteristic 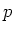 .
Let
.
Let  be a
be a 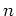 -dimensional semisimple Lie algebra over a field
-dimensional semisimple Lie algebra over a field  .
Let
.
Let 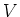 be a
be a 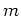 -dimensional
-dimensional  -module.
Let
-module.
Let 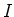 be the kernel of the representation
be the kernel of the representation 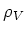 associated to
associated to 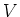 .
We assume
.
We assume
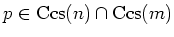 .
Then the Killing form
.
Then the Killing form
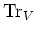 on
on 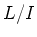 is non degenerate.
is non degenerate.
PROOF..

is semisimple and
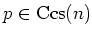
so

is non degenerate.
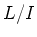
is also non-degenerate so
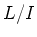
is semisimple. We may thus assume
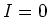
.
An ideal
of

is a solvable ideal. Since

is semisimple and
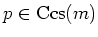
,
we have by
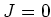
.
That means,
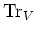
is non-degenerate on

.
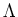
PROOF..
Since the question of existence of
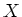
is described in terms of
existence of a solution of a set of linear equations,
we may assume that

is algebraically closed.
Let us denote by
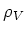
the representation of

associated to
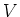
.
Then by replacing

by
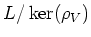
if necessary,
we may assume that the representation
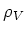
is faithful.
Note that since  is semisimple, it acts on
is semisimple, it acts on 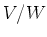 trivially.
trivially.
Let us first treat the case where 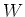 is irreducible.
Let
is irreducible.
Let 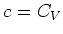 be a Casimir element with respect to
be a Casimir element with respect to 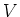 .
Since
.
Since  is acts on
is acts on 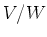 trivially,
trivially, 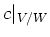 is equal to zero.
Thus
is equal to zero.
Thus
In particular,
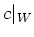
is not equal to zero.
On the other hand, by Schur's lemma,
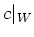
is equal to a scalar
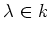
.
Thus
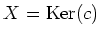
is a required object in this case.
We next come to general case. Let 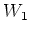 be the maximal proper
be the maximal proper  -submodule
of
-submodule
of  . Then we see that
. Then we see that
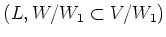 satisfies the
assumption of the lemma with
satisfies the
assumption of the lemma with 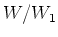 irreducible.
By the argument above, we therefore see that there exists an
irreducible.
By the argument above, we therefore see that there exists an  -submodule
-submodule 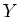 which contains
which contains 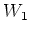 as a submodule of codimension
as a submodule of codimension 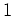 such that
such that
holds.
Since
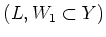
also satisfies the assumption of the lemma with
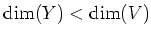
, we deduce by induction that the lemma holds in general.
LEMMA 5.52
Let  be a Lie algebra over a commutative ring
be a Lie algebra over a commutative ring  .
Then for any
.
Then for any  -modules
-modules 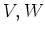 , each of the vector spaces
, each of the vector spaces
and
admits a structure of  -module. Namely,
-module. Namely,
PROOF..
Easy.
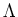
PROOF..
Let us define the following

-modules.
Then it is easy to see that the triple
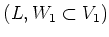
satisfies
the assumption of Lemma
5.51.
We therefore have an element

which satisfies the
following conditions.
-
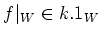 .
.
-
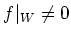 .
.
-
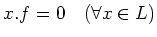 (In other words,
(In other words, 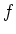 is a
is a  -linear homomorphism).
-linear homomorphism).
by dividing by a suitable element in

, we may assume
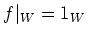
.
Then
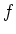
gives a splitting of the exact sequence
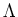



Next: Semi direct products of
Up: generalities in finite dimensional
Previous: examples
2009-03-06
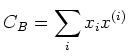
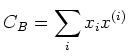
![]() , let us write the adjoint action of
, let us write the adjoint action of ![]() on
on ![]() by using
the basis
by using
the basis ![]() . Namely,
. Namely,
![$\displaystyle [a, x_i]=\sum_j c_{i}^{(j)}(a) x_j \qquad (c_{i}^{(j)}(a)\in k).
$](img573.png)
![$\displaystyle B(x^{(l)},[a, x_i])=\sum_j c_{i}^{(j)}(a) B(x^{(l)},x_j)= c_i^{(l)}(a)
$](img575.png)
![$\displaystyle [ x^{(l)},a]=\sum_i c_i^{(l)}(a) x^{(i)}.
$](img577.png)
![$\displaystyle \sum_i [a,x_i] x^{(i)} +\sum_i x_i[a, x^{(i)}]$](img579.png)
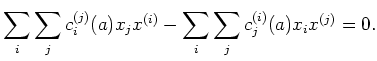
![]()
![]()
![]() is semisimple, it acts on
is semisimple, it acts on ![]() trivially.
trivially.
![]() is irreducible.
Let
is irreducible.
Let ![]() be a Casimir element with respect to
be a Casimir element with respect to ![]() .
Since
.
Since ![]() is acts on
is acts on ![]() trivially,
trivially, ![]() is equal to zero.
Thus
is equal to zero.
Thus
![]() be the maximal proper
be the maximal proper ![]() -submodule
of
-submodule
of ![]() . Then we see that
. Then we see that
![]() satisfies the
assumption of the lemma with
satisfies the
assumption of the lemma with ![]() irreducible.
By the argument above, we therefore see that there exists an
irreducible.
By the argument above, we therefore see that there exists an ![]() -submodule
-submodule ![]() which contains
which contains ![]() as a submodule of codimension
as a submodule of codimension ![]() such that
such that
![]()
![]() is completely reducible.
is completely reducible.![]()