


Next: -rationality
Up: Jordan-Chevalley decomposition of a
Previous: Jordan-Chevalley decomposition of a
DEFINITION 4.1
Let
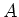
be a square matrix over a field

.
A
Jordan-Chevalley decomposition
(also called SN-decomposition) of
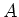
is a decomposition of
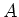
which satisfies the following conditions.
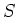 is semisimple
(that means, the minimal polynomial of
is semisimple
(that means, the minimal polynomial of 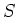 has only simple roots.)
has only simple roots.)
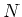 is nilpotent.
is nilpotent.
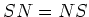
-
![$ S,N\in \overline{k}[A]$](img119.png)
A main objective of this section is to prove the following proposition.
PROPOSITION 4.2
For any square matrix 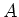 over a field
over a field  , there exists a unique
Jordan-Chevalley decomposition.
, there exists a unique
Jordan-Chevalley decomposition.
To prove it, we need some basic facts from linear algebra.
PROOF..
Since
![$ k[X]$](img126.png)
is an Euclidean domain, it is a principal ideal domain.
thus we see that there exists a polynomial
![$ l_1(X),l_2(X)\in k[X]$](img127.png)
such that
holds. We put
Then we see easily that
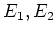
are mutually orthogonal projection. That means, we have
It is also easy to see that both
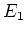
and
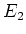
commute with
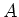
.
Now putting
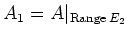
and
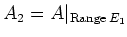
we see that
with
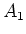
and
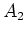
satisfying the required property.
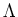
COROLLARY 4.4
Every square matrix 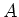 over a field
over a field  is similar to a direct sum of
square matrices
is similar to a direct sum of
square matrices
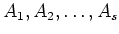 with each
minimal polynomial
with each
minimal polynomial 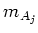 equals
to a power
equals
to a power 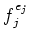 of a irreducible polynomial
of a irreducible polynomial 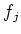 over
over  .
.
COROLLARY 4.5
When  is algebraically closed,
every square matrix
is algebraically closed,
every square matrix 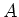 over a field
over a field  is similar to a direct sum of
square matrices
is similar to a direct sum of
square matrices
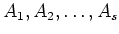 with each
minimal polynomial
with each
minimal polynomial 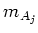 equals
to a power
equals
to a power
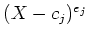 of a polynomial of degree
of a polynomial of degree 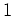 over
over  .
.
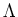
COROLLARY 4.6
A square matrix over a field  is semisimple if and only if it is
diagonalizable (similar to a diagonal matrix) over
is semisimple if and only if it is
diagonalizable (similar to a diagonal matrix) over
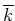 .
.
COROLLARY 4.7
Let 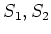 be semisimple square matrices of the same size over
be semisimple square matrices of the same size over  .
if
.
if 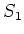 and
and 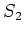 commute, then both
commute, then both 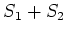 and
and 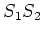 are also
semisimple.
are also
semisimple.
PROOF..
Using commutativity of
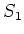
and
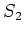
, we may easily see that
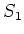
and
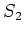
are simultaneously diagonalizable over
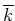
.
COROLLARY 4.8
Let  be a field. Let
be a field. Let 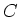 be a commutative subalgebra of
be a commutative subalgebra of 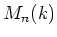 .
If
.
If 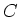 is generated by semisimple elements, then every element of
is generated by semisimple elements, then every element of 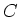 is also
semisimple.
is also
semisimple.
On the other hand we have
LEMMA 4.9
Let  be a field. Let
be a field. Let 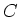 be a commutative subalgebra of
be a commutative subalgebra of 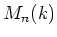 .
If
.
If 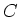 is generated by nilpotent elements, then every element of
is generated by nilpotent elements, then every element of 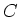 is also
nilpotent.
is also
nilpotent.
PROOF..
Easy.
COROLLARY 4.10
A Jordan-Chevalley decomposition (if there exists)
of a square matrix 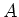 is unique.
is unique.
PROOF..
Let
be two Jordan-Chevalley decompositions. Then
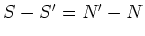
is a semisimple nilpotent element.
Thus
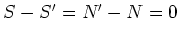
.
PROOF..
(of Proposition
4.2.)
It now remains to prove that Jordan-Chevalley decomposition of a square matrix
exists. By definition we may assume that

is algebraically closed.
In view of Corollary
4.5, we may then assume that
the minimal polynomial
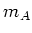
of
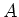
is of the form
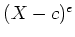
for some
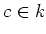
and
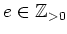
. Then
gives the required Jordan-Chevalley decomposition.
DEFINITION 4.11
Let

be a field.
For any square matrix
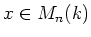
, we denote by
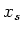
(respectively,
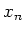
)
the semisimple (respectively, nilpotent) part of
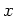
in the Jordan-Chevalley
decomposition of
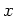
.
LEMMA 4.12
Let  be a field.
Let
be a field.
Let
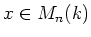 be a square matrix.
then we have
be a square matrix.
then we have
PROOF..
Follows easily from the uniqueness of the Jordan-Chevalley decomposition.
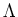
ARRAY(0x8eef838)ARRAY(0x8eef838)ARRAY(0x8eef838)ARRAY(0x8eef838)



Next: -rationality
Up: Jordan-Chevalley decomposition of a
Previous: Jordan-Chevalley decomposition of a
2009-03-06
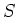 is semisimple
(that means, the minimal polynomial of
is semisimple
(that means, the minimal polynomial of 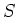 has only simple roots.)
has only simple roots.)
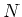 is nilpotent.
is nilpotent.
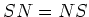
![$ S,N\in \overline{k}[A]$](img119.png)
![]()