

Next: の平方根
Up: 複素数について
Previous: 複素数について
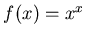 という関数は、
という関数は、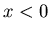 においては複素数の値を
とりそうだ、ということが本編で分かった。
だからそのグラフを描くには、複素数を図示する方法を知らなければならない。
この小節ではそれについて解説しよう。
においては複素数の値を
とりそうだ、ということが本編で分かった。
だからそのグラフを描くには、複素数を図示する方法を知らなければならない。
この小節ではそれについて解説しよう。
複素数 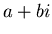 に対して、
に対して、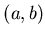 という平面上の
点を対応させることで、複素数を図示することができる。
そのように考えて、複素数を表現する平面をガウス平面とか、複素平面とかよぶ。
実はガウス平面の便利な点は、
単に複素数の一つ一つを平面上に図示できることだけではなくて、
次のように二つの複素数の足し算やかけ算を幾何学的に意味づけられる
ところにある。
という平面上の
点を対応させることで、複素数を図示することができる。
そのように考えて、複素数を表現する平面をガウス平面とか、複素平面とかよぶ。
実はガウス平面の便利な点は、
単に複素数の一つ一つを平面上に図示できることだけではなくて、
次のように二つの複素数の足し算やかけ算を幾何学的に意味づけられる
ところにある。
- 足し算:平行四辺形の法則
- かけ算:原点からの距離はかけ算。偏角は足し算。
ここで、複素数 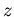 の「偏角」とは、ベクトルとしてみた
の「偏角」とは、ベクトルとしてみた 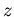 と、
x軸とのなす角度(を弧度法であらわしたもの)だ。
これを以下では
と、
x軸とのなす角度(を弧度法であらわしたもの)だ。
これを以下では 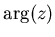 とかく。ついでに言うと、
とかく。ついでに言うと、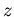 のベクトルとしての大きさ
は、
のベクトルとしての大きさ
は、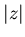 と書き、
と書き、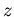 の絶対値、と呼ばれる。上に挙げたかけ算の標語を
もう一度これらの記号を使って書くと、
の絶対値、と呼ばれる。上に挙げたかけ算の標語を
もう一度これらの記号を使って書くと、
ということになる。
Yoshifumi Tsuchimoto
2000-04-12
![]() に対して、
に対して、![]() という平面上の
点を対応させることで、複素数を図示することができる。
そのように考えて、複素数を表現する平面をガウス平面とか、複素平面とかよぶ。
実はガウス平面の便利な点は、
単に複素数の一つ一つを平面上に図示できることだけではなくて、
次のように二つの複素数の足し算やかけ算を幾何学的に意味づけられる
ところにある。
という平面上の
点を対応させることで、複素数を図示することができる。
そのように考えて、複素数を表現する平面をガウス平面とか、複素平面とかよぶ。
実はガウス平面の便利な点は、
単に複素数の一つ一つを平面上に図示できることだけではなくて、
次のように二つの複素数の足し算やかけ算を幾何学的に意味づけられる
ところにある。