

Next: 指数関数の逆関数としての
Up: 対数関数の定義
Previous: 対数関数の定義
正の数の対数は易しい。というのも、
が
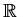 と
と
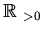 との間の一対一上への写像をあたえるため、
その逆写像として対数関数を定義すれば良いからである。
(良く知っている読者のための注意。「簡単である。」と言っているが、
実はこの一文の正当性を主張するには、
密かに、連続関数の中間値の定理が使われている。
さらに、対数関数の微分可能性等に言及するためには、
いわゆる逆関数の定理をもちいることになる。)
との間の一対一上への写像をあたえるため、
その逆写像として対数関数を定義すれば良いからである。
(良く知っている読者のための注意。「簡単である。」と言っているが、
実はこの一文の正当性を主張するには、
密かに、連続関数の中間値の定理が使われている。
さらに、対数関数の微分可能性等に言及するためには、
いわゆる逆関数の定理をもちいることになる。)
以下では、これを特別に
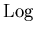 と書き、話の道標とすることにする。
と書き、話の道標とすることにする。
Yoshifumi Tsuchimoto
2000-04-12
![]() と書き、話の道標とすることにする。
と書き、話の道標とすることにする。