



Next: Algebra endomorphism and splitting
Up: First properties of Weyl
Previous: The quotient field of
Contents
definition of reduced trace and reduced norm
From a general theory of central simple algebra, we have a notion of
reduced traces and reduced norms. (See for example [1] for a theory
of reduced norms and reduced traces.)
It may be defined as follows.
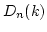 is a central simple algebra over
is a central simple algebra over 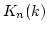 .
Let
.
Let 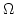 be a splitting field
be a splitting field 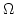 of
of 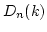 .
That means, we have an isomorphism of
.
That means, we have an isomorphism of  -algebras
-algebras
Then for each element 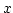 of
of 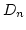 ,
it is known that the trace
,
it is known that the trace
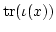 and the determinant
and the determinant
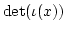 actually belongs to
actually belongs to 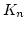 and that they do not actually depend
on the choice of the splitting field
and that they do not actually depend
on the choice of the splitting field 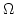 .
.
We call them reduced trace and reduced norm of 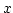 respectively.
respectively.
As we already saw in the previous section,
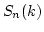 is a splitting algebra of
is a splitting algebra of  .
Thus we see that the quotient field
.
Thus we see that the quotient field 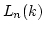 of
of 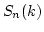 is one of the
splitting field of
is one of the
splitting field of 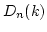 .
We have thus proved that reduced norm and reduced determinant of
.
We have thus proved that reduced norm and reduced determinant of
 actually lie in
actually lie in 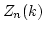 .
.




Next: Algebra endomorphism and splitting
Up: First properties of Weyl
Previous: The quotient field of
Contents
2003/3/3
![]() is a central simple algebra over
is a central simple algebra over ![]() .
Let
.
Let ![]() be a splitting field
be a splitting field ![]() of
of ![]() .
That means, we have an isomorphism of
.
That means, we have an isomorphism of ![]() -algebras
-algebras
![]() respectively.
respectively.
![]() is a splitting algebra of
is a splitting algebra of ![]() .
Thus we see that the quotient field
.
Thus we see that the quotient field ![]() of
of ![]() is one of the
splitting field of
is one of the
splitting field of ![]() .
We have thus proved that reduced norm and reduced determinant of
.
We have thus proved that reduced norm and reduced determinant of
![]() actually lie in
actually lie in ![]() .
.