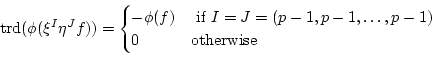
This is the same as Corollary 5. One may also prove this by using Corollary 2.
![]()
ARRAY(0x8ed5254)
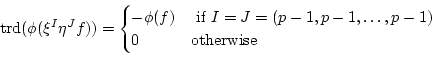
This is the same as Corollary 5. One may also prove this by using Corollary 2.
![]()
ARRAY(0x8ed5254)
For any index set
![]() ,
we denote by
,
we denote by ![]() the index set
the index set
![]() .
.
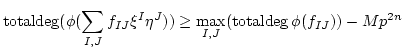
![]()
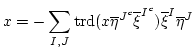
ARRAY(0x8ec301c)