代入の諸方法(1)

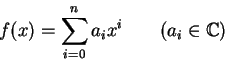
前節では、古典論と量子論の「対応」、 とくに通常の関数に微分作用素等の「作用素」 を対応させる話が出た。 このような「対応」のためには作用素の非可換性以外にも 解決されるべき問題がいくつかある。 このあたりの事情について少し触れておこう。

まずこのような「対応」の多くがしばしば「代入算」として 説明されることに注意しておく。 実際、関数はしばしば多項式の「極限」として得られ、 多項式については(作用素の積の順序の問題を別にすれば) 前節で述べたような「対応」を容易につけることができる。

議論に現れる作用素が一つだけの時には、この対応はとくに見やすい。 多項式

$$f(x)=\sum _{i=0}^{n} a_i x^i \quad \quad (a_i \in {\Bbb C})$$

に対しては、x を作用素 A に単に置き換えて、

$$f(A)=\sum _{i=0}^{n} a_i A^i$$

をつくれば良いのである。 この対応を連続に拡張する方法がいくつかあるが、 ここではいわゆる「Operator calculus」について述べよう。

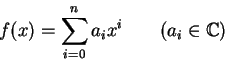
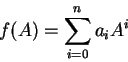
○自己共役な作用素に対する代入算

ヒルベルト空間 H 上の作用素 A が自己共役なら、A を $\mbox{${\Bbb R}$ }$ 上の任意の連続関数 f に代入することができる。

大学初年級の知識で、このことをある程度了解するために、 H が有限次元の時を考えてみることにしよう。 このときには、 A はユニタリ作用素で対角化される。 f(A) を求めるには A を対角化して対角線の各要素を f に代入すればいい。 もう少し詳しくいうと、次のようになる。

A が次のように対角化されているとする。

A=UDU^*

(U はユニタリ行列。D は対角行列。) このとき、任意の一変数多項式 f(x) に対して、

f(A)=Uf(D)U^*

がなりたつ。f(D) は D の各要素を f に代入することにより 直ちに求まる。

$$f({diag}(d_1,\dots,d_k\dots))={diag}(f(d_1),\dots,f(d_k),\dots)$$

この操作は、f が多項式以外の場合にも容易に拡張でき、 結局、H が有限次元の場合については $\mbox{${\Bbb R}$ }$ 上の任意の関数に H 上の自己共役作用素を「代入」することができる。

H が無限次元の時には、上の「対角化」は「スペクトル測度」 による「スペクトル分解」に置き換えることになる。 有限次元の時のように「対角要素」(スペクトル)は離散的に現れるとは限らず、 いわゆる「連続スペクトル」を考慮にいれなければならなくなる。 その結果さすがに全ての関数 f に作用素 A を代入するわけにはいかなくなるが、 f のボレル可測性を仮定すれば f(A) を定義することができる。 (我々が普通に考える関数は大抵ボレル可測である。)

上の議論でも察しがつくように、 f(A) は A のスペクトル集合 Sp(A) 上での f の値にのみ依存する。

代入算は Sp(A) 上の関数環と、A で「位相的に生成された」作用素代数との 環としての同型を与える。作用素代数の種々の問題が集合 Sp(A) の 問題に帰着されるのである。

作用素の数が増えた時にも、これらの作用素が互いに可換であるならば、 上のような議論が可能である。(線型代数の知識では、 「可換な対称行列は同時対角化可能」という定理がこれにあたる。)

例えば、Gel'fand による可換 C^* 代数の表現定理:

- 可換 C^* 代数はあるコンパクト集合 K 上の 連続関数全体のなす環と同型である。 -

はこのタイプの定理の代表的なものである。

可換環にその「スペクトル集合」を対応させるというアイディアは、 補強されてアファインスキームの理論につながっていくことになる。 これについては代数幾何学の成書を参照されたい。

○一般の作用素に対する代入算

上の議論で、「自己共役な」作用素について考察してみたが、 一般の作用素についてはどうであろうか。

A が正規、すなわち A とその共役作用素 A^* とが可換な場合には、 容易に上の議論に帰着できる。A^* が重要視されるのは、 Weierstrass の多項式近似定理(の複素領域版)

- 複素平面 ${\Bbb C}$ の任意のコンパクトな部分集合 K と その上の連続関数 f は, $z,\bar{z}$ の多項式で K 上一様に 近似できる。 -

にその源を求めることができる。(z の複素共役 $\bar{z}$ が 必要になる所がポイントである。)

z のみの多項式で近似できるのは K の内部で解析的な関数のみであり、 それに対応して 正規と限らない作用素 A はそのスペクトル集合の近傍で解析的な関数 には代入できることが示される。 (線型代数の知識でいえば、A は「対角化可能部分」S と「巾零部分」 Nの和(で、S と N は可換)というぐあいに書け、 f の Taylor展開を用いて

$$f(S+N)=f(S)+f'(S)N+\dots$$

という具合に書けることに当たる。 (ここの所は少し不正確に述べている部分があるが、 感覚を掴むための例であるので詳しくは述べない。)

なお、この節で述べたことは、 Bourbaki(本家!) 「スペクトル論」に詳しい。