

: 非可換環の「制限」
: 複素射影空間
: 余談:Fubini-Study 計量の形式的な導き方について
次節以降で、
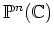 の Fubini-Study 計量 をシンプレクティック 商
の立場から見直したいのだが、この節ではその準備として
シンプレクティック多様体の一般論の初歩について復習しておく。
の Fubini-Study 計量 をシンプレクティック 商
の立場から見直したいのだが、この節ではその準備として
シンプレクティック多様体の一般論の初歩について復習しておく。
シンプレクティック多様体は非可換な object の「影」とみたいので、
シンプレクティック多様体の詳細な議論はさけ、粗筋のみを
追うことにする。
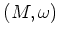 がシンプレクティック多様体であるとは、
次の諸条件を満たす時にいう。
がシンプレクティック多様体であるとは、
次の諸条件を満たす時にいう。
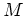 は実
は実 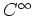 多様体である。
多様体である。
-
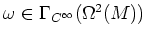 (実 2-形式).
(実 2-形式).
-
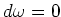
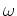 は非退化。
は非退化。
(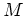 が 非退化な
が 非退化な 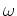 をもつためには、
をもつためには、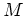 の次元は偶数でなければ
ならない。シンプレクティック多様体ばかりを対象として理論を
作る際には、部分空間や商空間をとる時に偶数次元づつ次元を下げなければならない。
このことは、シンプレクティック商の必要性の最初の暗示である。)
の次元は偶数でなければ
ならない。シンプレクティック多様体ばかりを対象として理論を
作る際には、部分空間や商空間をとる時に偶数次元づつ次元を下げなければならない。
このことは、シンプレクティック商の必要性の最初の暗示である。)
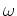 により、
により、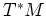 と
と 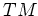 との間の同型写像
との間の同型写像 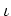 が得られる。
が得られる。
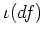 のことを
のことを 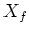 と書く。
と書く。
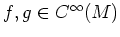 に対して、それらのポアソン括弧は、
に対して、それらのポアソン括弧は、
で定義される。
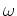 が
が 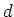 -closed であることから、
-closed であることから、
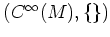 は Lie 代数であることが従う。
さらに、
は Lie 代数の拡大であることがわかる。
は Lie 代数であることが従う。
さらに、
は Lie 代数の拡大であることがわかる。
平成16年8月24日
![]() がシンプレクティック多様体であるとは、
次の諸条件を満たす時にいう。
がシンプレクティック多様体であるとは、
次の諸条件を満たす時にいう。
![]() により、
により、![]() と
と ![]() との間の同型写像
との間の同型写像 ![]() が得られる。
が得られる。
![]() のことを
のことを ![]() と書く。
と書く。
![]() に対して、それらのポアソン括弧は、
に対して、それらのポアソン括弧は、