


: 幾何学的ブラウアー群の方向への変形
: 曲面の非可換変形のいくつかの例について
: 交換関係の変更
目次
前節での話では 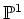 という「大域的な」座標変数
という「大域的な」座標変数 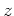 をもったスキーム
を使っているので
楽だったが、一般の場合はそうはいかない。
一般の交換関係の変更の様子を知るために、
話を ``analytic'' (ないし、formal)な場合にまで広げて、
二つの楕円曲線(というか、一次元複素トーラス)
をもったスキーム
を使っているので
楽だったが、一般の場合はそうはいかない。
一般の交換関係の変更の様子を知るために、
話を ``analytic'' (ないし、formal)な場合にまで広げて、
二つの楕円曲線(というか、一次元複素トーラス)
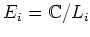 (
(
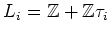 は
は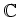 の maximal lattice)(
の maximal lattice)(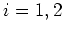 )
の積
)
の積
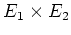 の変形について考えてみることにしよう。
今度は(トーラス全体で定義された関数という訳ではないが)平坦な
座標関数を用いることができる。
また、
の変形について考えてみることにしよう。
今度は(トーラス全体で定義された関数という訳ではないが)平坦な
座標関数を用いることができる。
また、
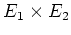 の双対2-formは(0 以外は)必ず非退化であり、
ある意味では最も「非特異」の語にふさわしいものが期待できそうである。
の双対2-formは(0 以外は)必ず非退化であり、
ある意味では最も「非特異」の語にふさわしいものが期待できそうである。
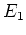 ,
, 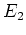 の平坦な座標関数をそれぞれ
の平坦な座標関数をそれぞれ 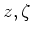 と書くことにする。
と書くことにする。
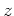 と
と 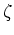 との交換関係を次のように変更しよう。
との交換関係を次のように変更しよう。
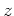 や
や 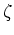 は周期関数ではないので
は周期関数ではないので 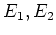 の関数とみなすことは
できない。そこで例えば
の関数とみなすことは
できない。そこで例えば 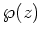 と
と
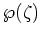 との交換関係が
どうなるかが問題になる。
(なお、以下の計算を間に合わせ的に正当化するには、
との交換関係が
どうなるかが問題になる。
(なお、以下の計算を間に合わせ的に正当化するには、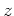 及び
及び 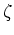 を
それぞれ
を
それぞれ 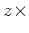 ,
, 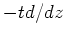 という
という
![$ {\Bbb C}((z)) /{\Bbb C}[z,z^{-1}] $](img182.png) 上の(可逆な)作用素と見倣し、
作用素の収束はその関数空間上の単純収束の位相を考えれば良い。
逆に言えば以下では
上の(可逆な)作用素と見倣し、
作用素の収束はその関数空間上の単純収束の位相を考えれば良い。
逆に言えば以下では 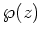 と擬微分作用素
と擬微分作用素
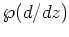 との
交換関係を計算していることになる。)
まず、上の式から一般に、
との
交換関係を計算していることになる。)
まず、上の式から一般に、
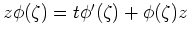 が
が 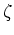 の多項式あるいはその極限で与えられるような
の多項式あるいはその極限で与えられるような 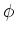 (以下このようなものを単に「式」と言い表す)について
成り立つ。とくに、
(以下このようなものを単に「式」と言い表す)について
成り立つ。とくに、
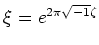 とおくと、
が成り立つことが分かる。これは、任意の
とおくと、
が成り立つことが分かる。これは、任意の 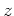 の「式」
の「式」 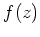 にたいして
が成り立つことを示しており、とくに、
にたいして
が成り立つことを示しており、とくに、
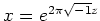 とおくと、
とおくと、
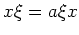 と書けることになる。マーニン[5] はこの交換関係から出発して、
テータ関数の量子版について論じている。その考察は(2次元とは限らない)
一般のトーラスの量子化にあたるものを関数環の位相まで込めて議論して
いることになっていて興味深いものであるが、
その全部をここで紹介するわけにもいかない。
そこでここではとくに
と書けることになる。マーニン[5] はこの交換関係から出発して、
テータ関数の量子版について論じている。その考察は(2次元とは限らない)
一般のトーラスの量子化にあたるものを関数環の位相まで込めて議論して
いることになっていて興味深いものであるが、
その全部をここで紹介するわけにもいかない。
そこでここではとくに 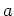 が特別の値をとる時について議論したい。
(実質的には [5]において 「
が特別の値をとる時について議論したい。
(実質的には [5]において 「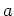 が 1の巾根の時」
として扱われている。)
が 1の巾根の時」
として扱われている。)
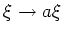 は
は 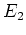 のある自己同型
のある自己同型 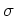 で
書けることに着目すると、これは
で
書けることに着目すると、これは
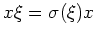 とかくこともできる。そこで、
とかくこともできる。そこで、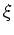 の任意の「式」に対して
が成り立つことになる。
いま、
の任意の「式」に対して
が成り立つことになる。
いま、 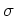 の位数
の位数 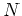 が有限であるとする(このような
が有限であるとする(このような
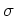 に対応する
に対応する 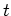 は
は 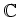 のなかで稠密である)と、
のなかで稠密である)と、
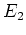 の上の「関数空間」(例えば、有理関数体)は
の上の「関数空間」(例えば、有理関数体)は 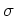 によって
固有分解を受ける。
によって
固有分解を受ける。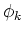 がそのひとつの固有関数、すなわち、
ならば、上の関係式は、
がそのひとつの固有関数、すなわち、
ならば、上の関係式は、
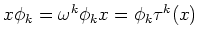 となり、
となり、
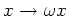 が
が 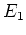 のひとつの自己同型
のひとつの自己同型 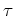 に対応すること
に着目すると、上と同様の議論により、任意の
に対応すること
に着目すると、上と同様の議論により、任意の 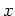 の「式」
の「式」 にたいし、
にたいし、
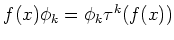 が成り立つことが分かる。この最後の式は、代数的に取り扱い可能であって、
次のような補題に一般化できる。
が成り立つことが分かる。この最後の式は、代数的に取り扱い可能であって、
次のような補題に一般化できる。
Lemma 8.1
Let
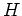
be a
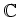
-bialgebra,
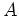
an
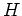
-module
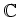
-algebra and
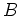
be an
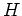
-comodule
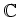
-algrebra.
Then
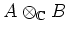
has a structure of a (unital associative)
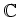
-algebra given by
where we denote the left comultiplication
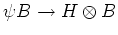
by
and multiplication of an element
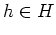
on
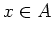
by
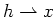
出て来る述語等については [1] を参照のこと。(とくに、「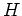 -module
-module
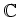 -algebra と言う述語に対しては注意が必要かと思われる。)
この補題は、
-algebra と言う述語に対しては注意が必要かと思われる。)
この補題は、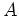 と
と 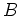 との間に交換関係を設定して、
との間に交換関係を設定して、
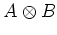 に
積を導入するには、bialgebra による action と coaction がそれぞれ
に
積を導入するには、bialgebra による action と coaction がそれぞれ
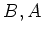 にあれば十分であることを示している。少し考えると分かるのだが、
にあれば十分であることを示している。少し考えると分かるのだが、
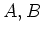 が有限次元の時などはこれは必要でもある。(これらの事実や上の補題
は基本的かつ簡単なのだがどこを引用すべきか分からなかった。土基にお教え
願えると幸いである。)
が有限次元の時などはこれは必要でもある。(これらの事実や上の補題
は基本的かつ簡単なのだがどこを引用すべきか分からなかった。土基にお教え
願えると幸いである。)
有限群
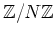 とその双対によるトーラスへの作用(平行移動)
をホップ代数で表現し、上の補題を適用すると上の議論と同等のことができる。
しかし、反省してみると、上の議論で、
とその双対によるトーラスへの作用(平行移動)
をホップ代数で表現し、上の補題を適用すると上の議論と同等のことができる。
しかし、反省してみると、上の議論で、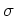 の
の 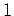 -固有空間は
-固有空間は
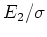 の関数空間と同一視でき、それらの元は変形された代数の中心に属するので、
容易に分かるように変形された環は
の関数空間と同一視でき、それらの元は変形された代数の中心に属するので、
容易に分かるように変形された環は
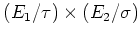 の
上の有限階数の代数の層のセクションと見倣すことができる。したがって、
残念ながら以上の考察のみからは Artin の予想の反例を得ることはできない。
トーラスの変形族のうち射影的なものが本当に上に挙げたものしか無いかどうかは
面白い問題だと思われる。
の
上の有限階数の代数の層のセクションと見倣すことができる。したがって、
残念ながら以上の考察のみからは Artin の予想の反例を得ることはできない。
トーラスの変形族のうち射影的なものが本当に上に挙げたものしか無いかどうかは
面白い問題だと思われる。
とりあえず、この場合には変形は ``analytic'' ないし ``formal''なカテゴリーで
うまく実現されており、その中の ``rational'' な点に対応しているもの(のみ?)
が代数的である。



: 幾何学的ブラウアー群の方向への変形
: 曲面の非可換変形のいくつかの例について
: 交換関係の変更
目次
平成15年9月1日
![]() という「大域的な」座標変数
という「大域的な」座標変数 ![]() をもったスキーム
を使っているので
楽だったが、一般の場合はそうはいかない。
一般の交換関係の変更の様子を知るために、
話を ``analytic'' (ないし、formal)な場合にまで広げて、
二つの楕円曲線(というか、一次元複素トーラス)
をもったスキーム
を使っているので
楽だったが、一般の場合はそうはいかない。
一般の交換関係の変更の様子を知るために、
話を ``analytic'' (ないし、formal)な場合にまで広げて、
二つの楕円曲線(というか、一次元複素トーラス)
![]() (
(
![]() は
は![]() の maximal lattice)(
の maximal lattice)(![]() )
の積
)
の積
![]() の変形について考えてみることにしよう。
今度は(トーラス全体で定義された関数という訳ではないが)平坦な
座標関数を用いることができる。
また、
の変形について考えてみることにしよう。
今度は(トーラス全体で定義された関数という訳ではないが)平坦な
座標関数を用いることができる。
また、
![]() の双対2-formは(0 以外は)必ず非退化であり、
ある意味では最も「非特異」の語にふさわしいものが期待できそうである。
の双対2-formは(0 以外は)必ず非退化であり、
ある意味では最も「非特異」の語にふさわしいものが期待できそうである。
![]() ,
, ![]() の平坦な座標関数をそれぞれ
の平坦な座標関数をそれぞれ ![]() と書くことにする。
と書くことにする。
![]() と
と ![]() との交換関係を次のように変更しよう。
との交換関係を次のように変更しよう。
![]() とその双対によるトーラスへの作用(平行移動)
をホップ代数で表現し、上の補題を適用すると上の議論と同等のことができる。
しかし、反省してみると、上の議論で、
とその双対によるトーラスへの作用(平行移動)
をホップ代数で表現し、上の補題を適用すると上の議論と同等のことができる。
しかし、反省してみると、上の議論で、![]() の
の ![]() -固有空間は
-固有空間は
![]() の関数空間と同一視でき、それらの元は変形された代数の中心に属するので、
容易に分かるように変形された環は
の関数空間と同一視でき、それらの元は変形された代数の中心に属するので、
容易に分かるように変形された環は
![]() の
上の有限階数の代数の層のセクションと見倣すことができる。したがって、
残念ながら以上の考察のみからは Artin の予想の反例を得ることはできない。
トーラスの変形族のうち射影的なものが本当に上に挙げたものしか無いかどうかは
面白い問題だと思われる。
の
上の有限階数の代数の層のセクションと見倣すことができる。したがって、
残念ながら以上の考察のみからは Artin の予想の反例を得ることはできない。
トーラスの変形族のうち射影的なものが本当に上に挙げたものしか無いかどうかは
面白い問題だと思われる。