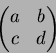Next: About this document ...
代数学 II 要約 No.1

定義 1.1 (環の定義)
集合
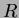
が環であるとは、足し算と呼ばれる写像
と掛け算と呼ばれる写像
が定義されていて次の性質を満たす時に言う。
- 1.
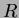 は足し算に関して可換群をなす。
は足し算に関して可換群をなす。
- 2.
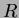 の積は結合法則を満たす。
の積は結合法則を満たす。
- 3.
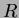 の足し算と掛け算は分配法則を満たす。
の足し算と掛け算は分配法則を満たす。
- 4.
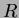 は積に関して単位元を持つ。
は積に関して単位元を持つ。
(☆)
レポート問題
(各回のレポート問題は、一問解けば十分です。
複数解いた場合には、そのなかで最良のものが
その回の点数になります。)
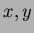 をそれぞれ諸君の入学年度および学生番号(98数理150氏の場合 x=98,y=150)
とし、行列
をそれぞれ諸君の入学年度および学生番号(98数理150氏の場合 x=98,y=150)
とし、行列 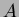 を
を
と決める。さらに、写像
![$\phi: {\Bbb C}[X] \to M_2({\Bbb C})$](img24.png) を、
を、
で定義する。このとき、
問題 1.1
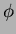
の核に属するような
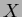
の多項式で、
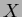
の二次式、三次式、四次式であるようなものの例をそれぞれ一つづつ
(計3つ)挙げなさい。 (それぞれなぜ
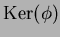
に入るか理由を書き添えること。)
問題 1.2
複素数を成分にもつ行列
が
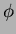
の像になるための必要条件を、
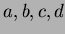
の一次式を使ってかきなさい。
(もちろん理由も添えること)
Yoshifumi Tsuchimoto
2000-04-11
![]()
![]() をそれぞれ諸君の入学年度および学生番号(98数理150氏の場合 x=98,y=150)
とし、行列
をそれぞれ諸君の入学年度および学生番号(98数理150氏の場合 x=98,y=150)
とし、行列 ![]() を
を