


Next: About this document ...
代数学 II 要約 No.4

定理4.1から4.3(定理3.1 から3.3 の再掲) は大変重要である。
定理 4.1
任意の体
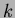
に対して、
![$k[X]$](img3.png)
は単項イデアル整域である。
すなわち、
![$k[X]$](img3.png)
は整域であって、しかもそのイデアルは全て単項イデアル
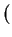
一つの元で生成されるイデアル
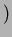
である。
定理 4.2
体
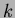
と、
![$k[X]$](img3.png)
の元
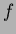
をとる。
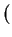
但し
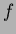
は定数ではないとする。
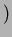
このとき、次は同値である。
- 1.
![$k[X]/(f)$](img7.png) は整域である。
は整域である。
- 2.
![$k[X]/(f)$](img7.png) は体である。
は体である。
- 3.
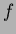 は既約多項式である。
は既約多項式である。
定理 4.3
体
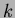
と、
![$k[X]$](img3.png)
の既約元
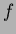
をとる。
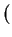
但し
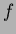
は定数ではないとする。
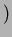
このとき、
![$K=k[X]/(f)$](img8.png)
とおき、
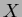
の
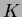
での同値類を
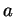
と書くと、
次のことが成り立つ。
- 1.
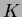 は
は 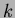 を含む体である。
を含む体である。
- 2.
![$K=k[a]$](img12.png) .
.
- 3.
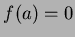 .
.
- 4.
-
![$[K:k]=\deg(f)\quad(\text{$f$\space の次数})$](img14.png) .
.
※上の定理は、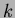 にあたらしく「
にあたらしく「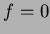 の根」
の根」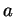 を一つ付け加えた
体を「作る」(構成する)ことができることを示している。
この操作を繰り返し行うことにより、さまざまな体を構成することができる。
こうやって構成した体同士の関係や、既存な体との関係が、次回のテーマになる。
を一つ付け加えた
体を「作る」(構成する)ことができることを示している。
この操作を繰り返し行うことにより、さまざまな体を構成することができる。
こうやって構成した体同士の関係や、既存な体との関係が、次回のテーマになる。
例 4.1
![$\mbox{${\Bbb Q}$ }[X]/(X^2-2)$](img16.png)
における、
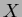
のクラスを
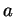
と書くと、

.
また、
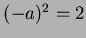
がなりたつ。
※上の二つの例で、
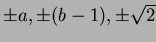 は全て二乗して
は全て二乗して 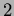 であるが、
べつにこれらの間に「等号」が成り立つ訳ではない。それはたとえば、行列
であるが、
べつにこれらの間に「等号」が成り立つ訳ではない。それはたとえば、行列
が 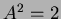 を満たすからといって、
を満たすからといって、
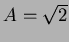 というわけではないのと
同様である。どの環を考えているか、その環にはどのぐらい元があるのか、
絶えず意識することが大事である。
というわけではないのと
同様である。どの環を考えているか、その環にはどのぐらい元があるのか、
絶えず意識することが大事である。
※但し、もちろん上の例の二つの体や、
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img27.png) には
深いつながりがある。実はこれらは体として同型である。
には
深いつながりがある。実はこれらは体として同型である。
注意: 上の問題で、 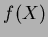 は
は
![$\mbox{${\Bbb Q}$ }[X]$](img34.png) の元として既約である。
このことの証明は難しくはないが、繁雑であるので、
ここでは証明せずに用いてもよい。(講義で類題について解説する。)
の元として既約である。
このことの証明は難しくはないが、繁雑であるので、
ここでは証明せずに用いてもよい。(講義で類題について解説する。)
Yoshifumi Tsuchimoto
2000-05-12
![]()
![]() にあたらしく「
にあたらしく「![]() の根」
の根」![]() を一つ付け加えた
体を「作る」(構成する)ことができることを示している。
この操作を繰り返し行うことにより、さまざまな体を構成することができる。
こうやって構成した体同士の関係や、既存な体との関係が、次回のテーマになる。
を一つ付け加えた
体を「作る」(構成する)ことができることを示している。
この操作を繰り返し行うことにより、さまざまな体を構成することができる。
こうやって構成した体同士の関係や、既存な体との関係が、次回のテーマになる。
![]() は全て二乗して
は全て二乗して ![]() であるが、
べつにこれらの間に「等号」が成り立つ訳ではない。それはたとえば、行列
であるが、
べつにこれらの間に「等号」が成り立つ訳ではない。それはたとえば、行列
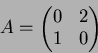
![]() には
深いつながりがある。実はこれらは体として同型である。
には
深いつながりがある。実はこれらは体として同型である。