


Next: About this document ...
代数学 II 要約 No.6

定義 6.1
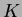
は体、
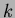
は
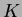
の部分体とする。このとき、
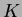
と
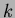
の間の
中間体とは、
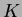
の部分体で、
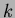
を含むもののことである。
中間体をうまく用いると、多項式の既約性の問題がやさしくなる場合がある。

定義 6.2
体
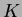
とその部分体
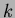
が与えられているとする。
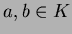
が
あったとき、
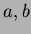
が
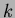
上の共役元であるとは、
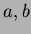
が
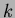
上代数的であって、
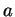
,
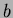
の
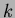
上の最小多項式が (定数倍を除いて)一致するときに言う。
定理 6.1
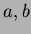
が
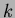
上共役ならば、体としての同型
![$k[a]\cong k[b]$](img20.png)
が存在する。
例 6.4
四つの元
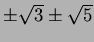
はどの二つも互いに
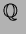
上共役である。
例 6.5
![$\sqrt[3]{5}$](img24.png)
と
![$\sqrt[3]{5}\omega$](img25.png)
(但し
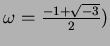
)
とは
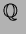
上互いに共役であるが、
![$\mbox{${\Bbb Q}$ }[\sqrt[3]{5}]$](img27.png)
上では二つは共役ではない。
定義 6.3
体
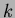
とその拡大体
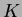
が与えられているとする。
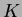
の
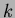
自己同型(あるいは、
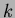
上の自己同型)とは、
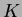
から
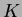
への同型
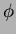
であって、
任意の
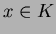
に対して
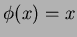
が成り立つものを言う。
例 6.6
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img4.png)
からそれ自身への準同型
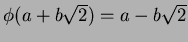
は
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img4.png)
の
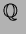
上の 自己同型である。
一般に、体 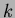 から 他の体
から 他の体 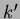 への同型
への同型
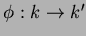 が与えられているとき、
が与えられているとき、
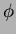 をつぎのように
をつぎのように ![$k[X]$](img34.png) から
から ![$k'[X]$](img35.png) への同型に伸ばすことができる。
これをこの講義では仮に
への同型に伸ばすことができる。
これをこの講義では仮に 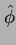 とかくことにする。(一般的な記号ではない。)
とかくことにする。(一般的な記号ではない。)
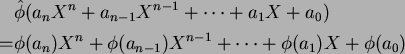
定理 6.2
体
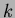
と、その拡大体
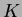
が与えられていて、さらに
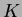
の
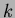
上の自己同型
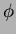
が与えられているとする。
もし
![$f\in k[X]$](img38.png)
,
![$g\in K[X]$](img39.png)
があって、
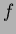
が(
![$K[X]$](img40.png)
のなかで)
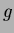
で割り切れれば、
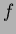
は (
![$K[X]$](img40.png)
のなかで)
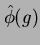
でも割り切れる。
この定理を用いれば、例6.2の 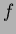 の既約性はもっと簡単に示すことができる。
の既約性はもっと簡単に示すことができる。
問題 6.2
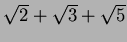
の
上の最小多項式を求め、
実際にそれが既約であることを示しなさい。
Yoshifumi Tsuchimoto
2000-05-23
![]()
![]()
![]() から 他の体
から 他の体 ![]() への同型
への同型
![]() が与えられているとき、
が与えられているとき、
![]() をつぎのように
をつぎのように ![]() から
から ![]() への同型に伸ばすことができる。
これをこの講義では仮に
への同型に伸ばすことができる。
これをこの講義では仮に ![]() とかくことにする。(一般的な記号ではない。)
とかくことにする。(一般的な記号ではない。)
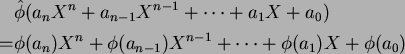
![]() の既約性はもっと簡単に示すことができる。
の既約性はもっと簡単に示すことができる。
![]() の
の
![]() 上の最小多項式をもとめ、
実際にそれが既約であることを示しなさい。
さらに、
上の最小多項式をもとめ、
実際にそれが既約であることを示しなさい。
さらに、
![]() と共役な
と共役な ![]() の元をすべて
もとめなさい。
の元をすべて
もとめなさい。
![]() の
の
![]() 上の最小多項式をもとめ、
実際にそれが既約であることを示しなさい。
さらに、
上の最小多項式をもとめ、
実際にそれが既約であることを示しなさい。
さらに、
![]() と共役な
と共役な ![]() の元をすべて
もとめなさい。
の元をすべて
もとめなさい。