代数学 II 要約 No.8

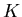
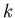
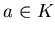
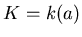
定義 8.1   体 $K$ が体 $k$ の単純拡大であるとは、ある $a\in K$ があって $K=k(a)$ が成り立つときに言う。

もし、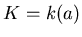$K=k(a)$ で、なおかつ $K$ が $k$ の有限次拡大ならば、 すでに述べたように $K=k[a]$ が成り立つ。

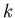
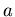
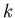
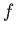
定理 8.1   体 $k$ とその有限次単純拡大体 $K=k[a]$ が与えられているとする。 $a$ の $k$ 上の最小多項式を $f$ とするとき、次のことが成り立つ。

1.

$\vert\operatorname{Aut}_k(K)\vert=\char93 \{x\in K; f(x)=0\}$.

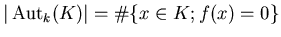2.

$\vert\operatorname{Aut}_k(K)\vert\leq \deg(f)\leq [K:k]$

次の三つの例と補題は前回の残りである。

例 8.1   $\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2}])=1.$

例 8.2   $\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2},\omega])=\frak{S}_3$ (三次対称群).

例 8.3   $\operatorname{Aut}_{\mbox{${\Bbb Q}$ }[\omega]}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2},\omega])={\mbox{${\Bbb Z}$ }}/3{\mbox{${\Bbb Z}$ }}$

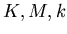
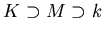
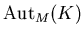
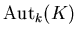
補題 8.1   三つの体 $K,M,k$ があって、 $K\supset M\supset k$ がなりたつとき、 $\operatorname{Aut}_M(K)$ は $\operatorname{Aut}_k(K)$ の部分群である。

問題 8.1   $\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[4]{5}])$ の位数を求めよ。

問題 8.2   $\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt{2+\sqrt{3}}])$ の位数を求めよ。