がなりたつ。
次の定理を証明するのを抜かしていました。すみません。 証明は簡単なので、以下では略証のみを書いておきます。
[証明]
![]() とおく。定義により、
とおく。定義により、
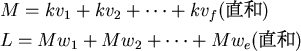
をみたすような
![]() が
存在する。
が
存在する。
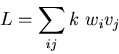
上の定理を使えば、例えば
![]() の 4次拡大
の 4次拡大 ![]() が
が
![]() の3次拡大を
含むことはないことなどがわかります。(なぜだか考えてみてください。)
の3次拡大を
含むことはないことなどがわかります。(なぜだか考えてみてください。)
なお、No.11 のレポートで、例えば
![]() にたいして、
にたいして、
![]() となるような
となるような
![]() を求めよ、という問題について、
「求め方が分からない(教えてもらってない?)から、解答できない。」
と答えた人がいますが、
たぶんそのような人でも、
を求めよ、という問題について、
「求め方が分からない(教えてもらってない?)から、解答できない。」
と答えた人がいますが、
たぶんそのような人でも、
![]() を示せ
を示せ
という問題にすれば解答できたと思われます。 ちょっとした考え方の変更で、本当は対処できる問題が 解けないのはもったいない話です。
土基善文