問題 5.1(前半)
![]() と
と
![]() との間の同型写像を一つ作りなさい。
との間の同型写像を一つ作りなさい。
(解答)
以下では多項式 ![]() の
の
![]() ,
,
![]() でのクラスを
それぞれ
でのクラスを
それぞれ
![]() という風に表記することにする。
という風に表記することにする。
![]() の元
の元 ![]() を、
を、
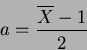
![\begin{alignat*}{2}
\varphi:
&\mbox{${\Bbb Q}$ }[X]/(X^2+X+1)&\to &\mbox{${\Bbb Q}$ }[X]/(X^2+3)\\
&\widetilde{p(X)} &\mapsto &p(a)
\end{alignat*}](img8.png)
(考え方)
![]() と
と
![]() のように、同じ集合
のように、同じ集合
![]() を
二つの異なるやり方で類別することは、よく行われることではあるが、
諸君はかなり混乱していたようである。
したがって、以下ではちょっと記号を変えて、
を
二つの異なるやり方で類別することは、よく行われることではあるが、
諸君はかなり混乱していたようである。
したがって、以下ではちょっと記号を変えて、
順を追って見てみよう。
[step 1]
![]() では、
では、 ![]() は
は
![]() と
同じ役目をし、
と
同じ役目をし、
![]() では、
では、![]() は
は ![]() と
同じ役目をしている。
と
同じ役目をしている。![]() が両方にでて来る所がポイントである。
が両方にでて来る所がポイントである。
[step 2]
互いに歩み寄ってみる。
step 1から、
![]() では、
では、
![]() が、
が、![]() と
同じ役目をしているし、
と
同じ役目をしているし、
![]() では、
では、
![]() が
が
![]() の役目をしている。
の役目をしている。
この問いではどちらの体からでも他方の体に向けての 同型写像が定義できる。その定義のもとになるのはこの考察である。
[step 3] 同じ役目をしているもの同士を対応させる。
ここでは考えをしぼるために、
![]() から
から
![]() への対応を考えることにしよう。このさい、基本的になるのは、
への対応を考えることにしよう。このさい、基本的になるのは、
![]() はどの元に対応させるべきか。
はどの元に対応させるべきか。
である。![]() と同じ働きをする元に対応させねばならない。
step 2 から、
と同じ働きをする元に対応させねばならない。
step 2 から、
![]() を対応させればよかろう、
ということになる。
を対応させればよかろう、
ということになる。
[step 4] ![]() に
に
![]() を対応させるとして、
あとのものはどう対応するのか。
対応が準同型になるためには、
を対応させるとして、
あとのものはどう対応するのか。
対応が準同型になるためには、
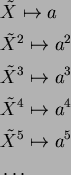
と対応せねばならない。このことから、たとえば、
しかし、今回のレポートではわけもわからずに「猿真似」して 変な式を書いてある答案も多かった。
[step 5] 対応はうまく定義されているか?
ようは、
あとは解答に述べた通りである。
(後半)
![]() の
の
![]() 上の最小多項式を
求めなさい。
上の最小多項式を
求めなさい。
実際、
![]() はこの多項式の根である。
はこの多項式の根である。
この多項式が
![]() 上既約であることは、次のようにしてわかる。
もし、この多項式(二次式)が
上既約であることは、次のようにしてわかる。
もし、この多項式(二次式)が
![]() 上既約でなければ、
上既約でなければ、
![]() のなかに根
のなかに根 ![]() をもつはずである。この
をもつはずである。この ![]() に対して、
に対して、
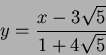
(考え方)