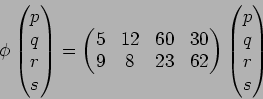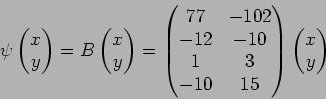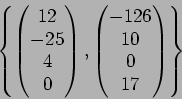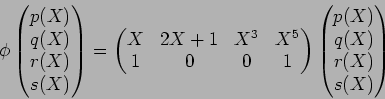Next: About this document ...
代数学特論 I 要約 No.9
今日のテーマ:

定義 9.1

-加群
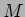
が与えられているとする。
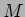
の部分集合
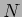
が
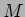
の

-部分加群
であるとは、
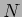
が
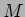
の部分加群で、かつ

の作用について閉じているときに
いう。
いいかえると、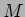 の
の  -部分加群とは
「
-部分加群とは
「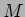 の部分集合で
の部分集合で  -加群の構造を持つもの」である。
(ただし、
-加群の構造を持つもの」である。
(ただし、 -加群としての構造は
-加群としての構造は 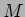 のものを制限して
得られるものでなければならない。)
のものを制限して
得られるものでなければならない。)
補題 9.1
環

と

-加群
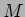
が与えられているとする。
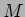
の元

に対して、次のことは同値である。
- 1.
-
 は
は 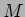 を生成する。
を生成する。
- 2.
-
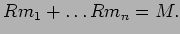
- 3.
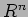 から
から 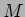 への写像
への写像
は全射である。
定義 9.2
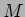
が(

-加群として)有限個の元で生成されるとき、
「
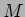
は有限生成

-加群である」という。
定義 9.3
可換環

の任意のイデアルが有限生成であるとき、

はネーター環であるという。
PID は当然ネーター環である。とくに整数全体のなす環
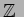 および
体
および
体 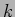 上の1変数多項式環
上の1変数多項式環 ![$k[X]$](img12.png) はネーター環である。
一般に、ネーター環
はネーター環である。
一般に、ネーター環  上の
上の 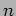 -変数多項式環
-変数多項式環
![$R[X_1,\dots, X_n]$](img14.png) は
ネータ環であることが知られている(ヒルベルトの基定理)。
これについては、本講義で時間があれば証明することにする。
は
ネータ環であることが知られている(ヒルベルトの基定理)。
これについては、本講義で時間があれば証明することにする。
 のイデアルと一般の
のイデアルと一般の  加群の間には次のような関係がある。
加群の間には次のような関係がある。
補題 9.3
可換ネーター環

上の有限生成

加群
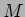
が与えられているとする。
このとき、
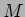
の

-部分加群は必ず

上有限生成である。
系 9.1
可換ネーター環

上の有限生成

加群
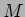
に対して
次のような

-加群の完全系列が存在する。
但し、一般に  -加群の完全系列
-加群の完全系列
とは、
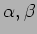 ともに
ともに  -加群の準同型であって、
-加群の準同型であって、
が成り立つときにいう。
従って、 (※)が完全系列であるとは、
- 1.
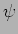 は 全射である。
は 全射である。
- 2.
-
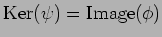
という二つのことを言っていることになる。
とくに、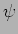 は
は
という同型を誘導する。
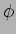 は
は 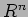 から
から 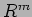 への
への  -準同型であるから、行列の形で書ける。
この行列の標準型を求めるのが、次回の課題である。
-準同型であるから、行列の形で書ける。
この行列の標準型を求めるのが、次回の課題である。
(例)
 上の加群の準同型
上の加群の準同型
を
で定義する。このとき、
- 1.
 は 全射である。実際、
は 全射である。実際、
とおくと、
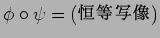 である。
である。
- 2.
-
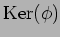 の生成元としては、例えば次のものをとることができる。
の生成元としては、例えば次のものをとることができる。
実際、簡単な行列式の計算により、
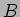 の列ベクトルに上の二つのベクトルを加えたものは
の列ベクトルに上の二つのベクトルを加えたものは 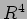 を
生成することがわかる。
を
生成することがわかる。
問題 9.1
![$R={\Bbb C}[X]$](img36.png)
上の加群の準同型
を
で定義する。このとき、
- 1.
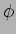 は 全射であることを示しなさい。
は 全射であることを示しなさい。
- 2.
-
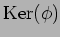 を生成するような有限集合の例をあげなさい。
を生成するような有限集合の例をあげなさい。



Next: About this document ...
Yoshifumi Tsuchimoto
2000-11-24
![]()
![]() および
体
および
体 ![]() 上の1変数多項式環
上の1変数多項式環 ![]() はネーター環である。
一般に、ネーター環
はネーター環である。
一般に、ネーター環 ![]() 上の
上の ![]() -変数多項式環
-変数多項式環
![]() は
ネータ環であることが知られている(ヒルベルトの基定理)。
これについては、本講義で時間があれば証明することにする。
は
ネータ環であることが知られている(ヒルベルトの基定理)。
これについては、本講義で時間があれば証明することにする。
![]() のイデアルと一般の
のイデアルと一般の ![]() 加群の間には次のような関係がある。
加群の間には次のような関係がある。![]() -加群の完全系列
-加群の完全系列
![]() 上の加群の準同型
上の加群の準同型