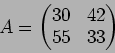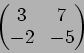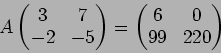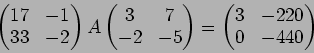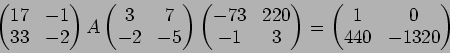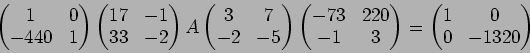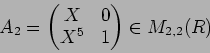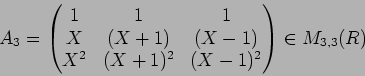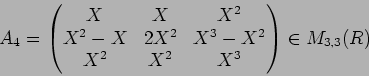Next: About this document ...
代数学特論 I 要約 No.10
今日のテーマ:
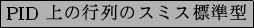
(記法)
可換環 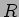 について、次のような記号を用いる。
について、次のような記号を用いる。
定理 10.1
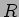
はPIDで、
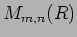
の元
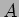
が与えられているとする。
このとき、
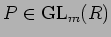
と
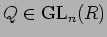
とをうまく与えれば、
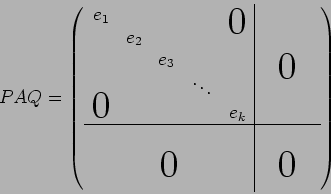
PAQ は次のような形にできる。
(
ただし,
 は
は 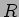 の元で、
の元で、
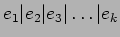 がなりたつ。)
がなりたつ。)
この定理の証明は本質的には 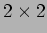 行列の話だけで理解できる。
行列の話だけで理解できる。
例えば
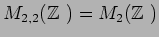 の元
の元
で定義する。まず  と
と 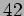 (第1行)とでユークリッドの互除法(gcd は6)を行い、
(第1行)とでユークリッドの互除法(gcd は6)を行い、
という式を得る(この式にあたるものは一般のPID 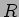 ではイデアルの議論から得る。)
二番目の式から
ではイデアルの議論から得る。)
二番目の式から
は
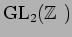 の元であることがわかる。
の元であることがわかる。
今度は、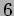 と
と  (第1列)とで同様なことを行う。
(第1列)とで同様なことを行う。
今度は再び1行で同様な操作を行う。
(1,1)-成分が段々``小さく''なっていくことに注意。
最後にもう一度第一列について同じことをする。
結局、
と置けばよい。
うえのような計算がいつでも止まることをいうには、
「PID のイデアルの増大列がいつでもどこかでとまる」という事実に
注意すればよい。この事実自体は代数Iですでに出てきているはずである。
全く同じことをするのはばかばかしいので、
あとあとのためも考えてこの事実の拡張である、
一般のネーター環の特徴付けについての補題を証明する。
補題 10.1
- 1.
- 可換ネーター環
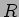 のイデアルの増大列
のイデアルの増大列
は必ずどこかで止まる。すなわち、ある 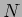 があって、そこから先は
があって、そこから先は
がなりたつ。
- 2.
- 逆に、可換環
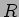 が「
が「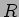 のイデアルの増大列は必ずどこかで止まる」
という性質をもてば、
のイデアルの増大列は必ずどこかで止まる」
という性質をもてば、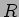 はネーター環である。
はネーター環である。
問題 10.1
![$R={\Bbb C}[X]$](img31.png)
とする。
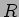
上の行列
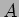
を下のように決めるとき、
定理10.1 の
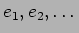
にあたるものをそれぞれ求めよ。
(理由付けをきちんと書いてあれば、とくに
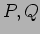
を求める必要はない。)
- 1.
-
- 2.
-
- 3.
-
(ヒント:
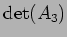 はいくらか?)
はいくらか?)
- 4.
-



Next: About this document ...
Yoshifumi Tsuchimoto
2000-12-04
![]()
![]() について、次のような記号を用いる。
について、次のような記号を用いる。
![]() は
は ![]() の元で、
の元で、
![]() がなりたつ。)
がなりたつ。)
![]() 行列の話だけで理解できる。
行列の話だけで理解できる。
![]() の元
の元