


Next: About this document ...
代数学特論 I 要約 No.13
今日のテーマ:

まず次の補題の証明が前回不十分だったので
補足しておく
補題 13.1
可換環
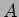
にたいして
また,
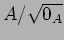
は
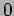
以外に巾零元をもたない。
もう一つ、補足的な補題をあげておく。
補題 13.2
![$k[X]$](img6.png)
加群
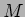
が
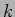
上有限生成なら、ある
![$f\in k[X]$](img9.png)
があって、
すべての
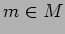
に対して
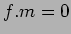
がなりたつ。
したがって、
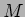
は
![$k[X]/(f)$](img12.png)
加群ともみなせる。
したがって ![$k[X]/(f)$](img12.png) を直積分解することにより
を直積分解することにより 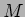 の構造が
単純化されるわけである。
の構造が
単純化されるわけである。
あとはここまで述べたことのまとめといくつかの注意を箇条書にしてみる。
まとめ
- 1.
- 「有理整数環
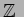 」、 および「体
」、 および「体 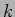 上の多項式環
上の多項式環 ![$k[X]$](img6.png) 」はPIDである。
」はPIDである。
- 2.
- PID
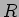 をそのイデアル
をそのイデアル
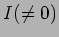 で割ったものは、
で割ったものは、
と直積分解され、それぞれの
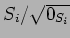 は体になる。
は体になる。
- 3.
![$R=k[X]$](img18.png) のときには、上の
のときには、上の
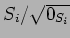 は
は 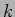 の代数拡大である。
の代数拡大である。
- 4.
- 逆に
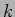 上の分離的な有限次代数拡大体は 必ず
上の分離的な有限次代数拡大体は 必ず ![$k[X]/(f)$](img12.png) (
(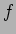 は
は ![$k[X]$](img6.png) の既約元)としてえられる。
の既約元)としてえられる。
- 5.
- 巾零元の存在は無視できないが、「無限小解析」的な処理で
切り抜けられるときもある。
- 6.
- PID 上の有限生成加群の様子は単因子論によりかなり精密にわかる。
- 7.
- とくに、有限生成アーベル群は巡回群の直和である。
- 8.
![$k[X]$](img6.png) 加群で、
加群で、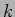 上有限次元であるものに対して
同様な議論を使うことにより、行列のジョルダンの標準型を導き出すこともできる。
上有限次元であるものに対して
同様な議論を使うことにより、行列のジョルダンの標準型を導き出すこともできる。
なお、試験はまだ具体的には考えていないが、
環の直積分解と行列のジョルダンの標準型の絡みについて出題する予定である。
Yoshifumi Tsuchimoto
2001-01-16
![]()