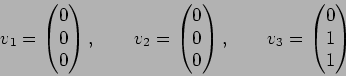![]()
 への
への
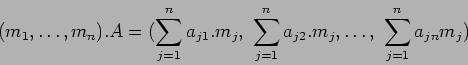
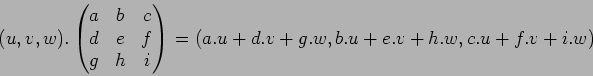
(解説):
![]() のことを略して
のことを略して![]() とかく。
とかく。
![]() が
が ![]() から
から ![]() まで動き回っているわけであるが、
このような略し方は諸君は数理科学英語ゼミナールでおなじみなはずである。
以下のそれぞれの式でどの変数が動き回るかにはとくに注意を要する。
それでは分かりにくいと思う人は
まで動き回っているわけであるが、
このような略し方は諸君は数理科学英語ゼミナールでおなじみなはずである。
以下のそれぞれの式でどの変数が動き回るかにはとくに注意を要する。
それでは分かりにくいと思う人は
![]() と
と ![]() を使う書き方を貫いてもよいが、かなり繁雑になることを
覚悟せねばならない。
和の記号
を使う書き方を貫いてもよいが、かなり繁雑になることを
覚悟せねばならない。
和の記号 ![]() がうまく使えること、
とくにどの添字に付いて和をとっているかが大事で、
この問題ではそこが一番のポイントである。
(というかそれ以外に問題はなかろう)
(答え):
がうまく使えること、
とくにどの添字に付いて和をとっているかが大事で、
この問題ではそこが一番のポイントである。
(というかそれ以外に問題はなかろう)
(答え):
![]() とすると、
とすると、

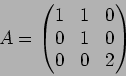
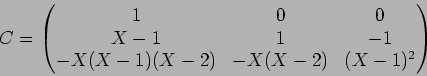
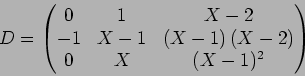
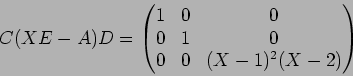
この状況の下で、
本問題はちょっとややこしかったかも知れない。
テンソル積を避けたため、![]() に二つの役割を背負わせているところが
いやらしい。
とくに、
に二つの役割を背負わせているところが
いやらしい。
とくに、
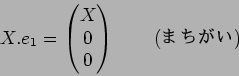
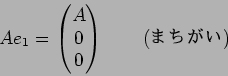
(答え):
1.
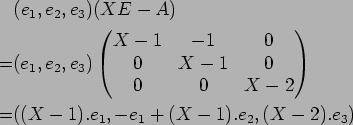
ここからが大事で、
問題にあるように ![]() の
の
![]() への作用は
への作用は ![]() によるかけ算である。
したがって、
によるかけ算である。
したがって、
2. これは単純計算である。一番時間をとるところであるが、
ここのところは正解率が高かった。答えだけ記すと
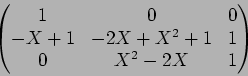
なお、諸君の解答の中で、![]() が変数ではなく、
が変数ではなく、
![]() の元かのごとく
あつかっている物があったが、それはそのままでは間違いである。
(正当化する方法もあるが、この問題はそのようなテクニックを使うほどの
ものではないし、
その解答を書いた人がそのテクニックを駆使しているとは考えにくい。)
の元かのごとく
あつかっている物があったが、それはそのままでは間違いである。
(正当化する方法もあるが、この問題はそのようなテクニックを使うほどの
ものではないし、
その解答を書いた人がそのテクニックを駆使しているとは考えにくい。)
3.
この問題は簡単すぎたので諸君も答えにくかったのかも知れない。
![]() の定義式から、
の定義式から、
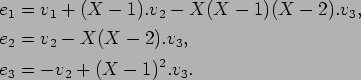
4.
これは 2. の結果を使う。
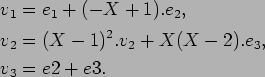
であり、1. と同様に計算すれば、