


Next: About this document ...
代数学 II 要約 No.1

「体上の多項式環のイデアル」という少し抽象的に見えるものが、
実は代数的集合と呼ばれる集合と対応していることを理解し、
その対応関係によってイデアルの種々の性質のもつ意味を直感的に
とらえられるようになる。
今日のテーマ:

次の定義と例は代数学C(コア),代数学I で既に知っているはずなので、
忘れた人は復習しておいて下さい。
定義 1.1 (復習)
- 1.
- 環とは、そのなかで加減乗算が自由にできるような集合である。
- 2.
- 体とは、環であってさらに
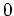 以外の元の逆元がまた
その中に含まれるような集合である。
以外の元の逆元がまた
その中に含まれるような集合である。
例 1.1
- 1.
- 有理数全体の集合
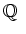 ,
実数全体の集合
,
実数全体の集合
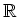 ,
複素数全体の集合
,
複素数全体の集合 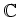 はそれぞれ体である。
はそれぞれ体である。
- 2.
- 整数全体の集合
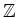 は環ではあるが、体ではない。
は環ではあるが、体ではない。
- 3.
- 自然数全体の集合
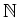 は環ですらない。
は環ですらない。
定義 1.2
環
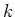
と正の整数
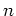
が与えられているとする。このとき、
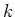
の元を係数にもつ
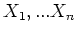
の多項式の全体のなす集合は
環になる。
この環のことを、
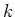
上の
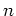
変数多項式環とよび、
![$k[X_1,X_2,\dots,X_n]$](img12.png)
で
あらわす。
(この講義ではおもに
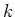
が体の場合を扱うが、場合によっては
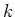
が環の場合の
余地を残しておいた方がよい。)
(注意)
変数のなまえは必ずしも
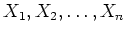 にしなければならないわけではない。
たとえば二変数(
にしなければならないわけではない。
たとえば二変数(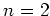 )
の時には
)
の時には 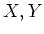 ,
3変数の時には
,
3変数の時には 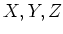 を変数に用いた方が
添字を書かなくてよい分だけ楽だろう。
を変数に用いた方が
添字を書かなくてよい分だけ楽だろう。
定義 1.3
体
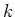
と正の整数
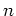
が与えられているとする。
![$k[X_1,X_2,\dots,X_n]$](img12.png)
の部分集合
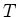
に対して、
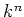
の部分集合
を
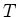
の共通零点の集合と呼ぶ。
問題 1.1
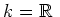
で
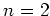
のときについて、
![$\mbox{${\Bbb R}$ }[X,Y]$](img34.png)
の部分集合
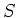
の例を
自分で考えて、その
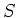
に対する
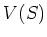
を図示しなさい。
(なぜそういうグラフになるのか、簡単な理由もそえること)
(あまり難しい例を考えられても採点が大変であるから
手頃のものでよいが、少なくとも他の人の解答と重ならないぐらい
の関数を用いるように努力すること。)
Yoshifumi Tsuchimoto
2001-04-16
![]()
![]()
![]() にしなければならないわけではない。
たとえば二変数(
にしなければならないわけではない。
たとえば二変数(![]() )
の時には
)
の時には ![]() ,
3変数の時には
,
3変数の時には ![]() を変数に用いた方が
添字を書かなくてよい分だけ楽だろう。
を変数に用いた方が
添字を書かなくてよい分だけ楽だろう。