


Next: About this document ...
代数学 II 要約 No.2
今日のテーマ:
前回プリントには書かなかったが、この講義ではとくに断らない限り「環」といえば
単位元を持つ可換環のことを意味する。
(なお、老婆心ながら、前回の「定義1.1」はちゃんとした定義ではない。
正確な定義は代数学C または代数学Iの講義で学んでいるはずである。)
(注意)
一般に、環 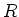 の元
の元
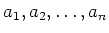 が与えられているとき、
が与えられているとき、
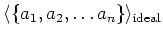 のことを単に
のことを単に
と丸括弧を使って書くことが多い。一般に数学では丸括弧に特別な意味をもたせることは
あまりないが、この「...で生成されるイデアル」は例外である。
数学ではよく用いられるし、楽でもあるので、本講義でもこの記号を用いることが
あるが、混乱しないように十分注意すること。
補題 2.1
体
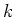
と正の整数
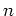
が与えられているとする。
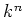
の部分集合
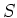
にたいして、
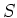
上で
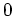
になる多項式の全体
は
![$k[X_1,X_2,\dots,X_n]$](img17.png)
のイデアルである。
補題 2.2
体
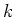
と正の整数
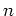
が与えられているとする。
![$R=k[X_1,X_2,\dots,X_n]$](img18.png)
の部分集合
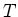
に対して、
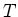
の共通零点の集合
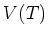
は
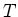
で生成された
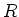
のイデアル
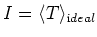
の共通零点の集合
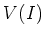
と一致する。
系 2.1
体
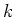
と正の整数
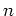
が与えられているとする。
![$R=k[X_1,X_2,\dots,X_n]$](img18.png)
の部分集合
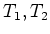
があって、もし
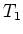
で生成された
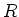
のイデアルと
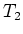
で生成された
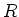
のイデアルが
一致する、すなわち
が成り立つならば、
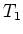
の共通零点の集合と
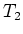
の共通零点の集合は
一致する。すなわち
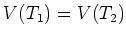
である。
上の理由から、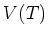 は
は 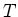 がイデアルのときのみを考えればじゅうぶんである。
一般に、
がイデアルのときのみを考えればじゅうぶんである。
一般に、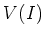 の形の集合を代数的集合と呼ぶ。
の形の集合を代数的集合と呼ぶ。
(注意)
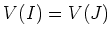 だからといって
だからといって 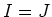 とは限らない。
とは限らない。
補題 2.3
体
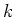
と正の整数
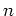
をきめ、
![$R=k[X_1,\dots X_n]$](img29.png)
とおく。
このとき、
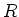
のイデアルの零点集合に対して次の諸式が成り立つ。
- 1.
-
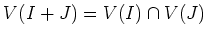
- 2.
- もっと一般に
- 3.
-
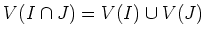
- 4.
-
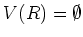
- 5.
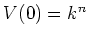
系 2.2
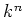
は、代数的集合の全体を閉集合として、位相空間をなす。
この位相のことを Zariski 位相と呼ぶ。
Zariski 位相は代数幾何学で基本的な役割を果たす。
この位相は(よく使われる位相のなかでは珍しく)Hausdorff 空間ではない。
問題 2.1
- 1.
-
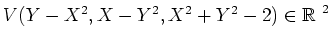 を図示しなさい。
を図示しなさい。
- 2.
- イデアルの等式
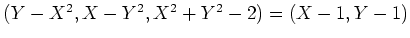 を証明しなさい。
を証明しなさい。
(注意)
1. は 2. を考える上でヒントにはなるが、2.の証明は 1. とは別に
付ける必要がある。
Yoshifumi Tsuchimoto
2001-05-01
![]()
![]() の元
の元
![]() が与えられているとき、
が与えられているとき、
![]() のことを単に
のことを単に
![]() は
は ![]() がイデアルのときのみを考えればじゅうぶんである。
一般に、
がイデアルのときのみを考えればじゅうぶんである。
一般に、![]() の形の集合を代数的集合と呼ぶ。
の形の集合を代数的集合と呼ぶ。
![]() だからといって
だからといって ![]() とは限らない。
とは限らない。