各 ![]() に対して S-多項式
に対して S-多項式
![]() を
を
![]() で割った余り
は
で割った余り
は ![]() である。
(この時点では余りは一意的かどうかわからないので、
余りは「うまく割った余り」の
意味である)
である。
(この時点では余りは一意的かどうかわからないので、
余りは「うまく割った余り」の
意味である)
各 ![]() に対して S-多項式
に対して S-多項式
![]() を
を
![]() で割った余り
は
で割った余り
は ![]() である。
(この時点では余りは一意的かどうかわからないので、
余りは「うまく割った余り」の
意味である)
である。
(この時点では余りは一意的かどうかわからないので、
余りは「うまく割った余り」の
意味である)
証明のキモは、
(キモ)
![]() の元
の元 ![]() をとると、
をとると、![]() は(
は(![]() の元だから)
の元だから)
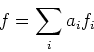
というところにある。![]() が
が ![]() にも属するためには
このような表現の最高次の部分はキャンセルせざるを得ず、そこで S-多項式が
登場するわけだ。(「最小になるもの」の存在は少しトリッキーである。)
にも属するためには
このような表現の最高次の部分はキャンセルせざるを得ず、そこで S-多項式が
登場するわけだ。(「最小になるもの」の存在は少しトリッキーである。)
この補題を見れば、グレブナ基底さえ分かれば、割り算の余りを見るだけで イデアルに入るかどうかがわかることになる。
グレブナ基底を求めるには、
生成元から出発してそれらの ![]() 多項式を割った余りをさらに付け加えて行けばよい。
この操作がいつかは止まること、さらには体上の多項式環の任意のイデアルは
実は有限個の元で生成されること、は、また余裕があれば述べることにする。
多項式を割った余りをさらに付け加えて行けばよい。
この操作がいつかは止まること、さらには体上の多項式環の任意のイデアルは
実は有限個の元で生成されること、は、また余裕があれば述べることにする。
レポート問題は1または2を選択すること。(1,はグレブナ基底を使わなくてもよい問題、 2. はグレブナ基底の問題である。)両方選択してもよいが、 評価されるのはどちらかよい方のみである。(したがって、「分かりません」 と書くだけの解答ならば二つ書いても無意味である。)
1.,2. ともに純粋に計算問題だが、多分 ![]() の概形を書いてみる方が
計算の目標がたてやすいだろう。
の概形を書いてみる方が
計算の目標がたてやすいだろう。