- 1.
-
![$R=\mbox{${\Bbb R}$ }[X]$](img4.png) で
で 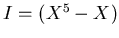 の場合。
の場合。
- 2.
-
![$R=\mbox{${\Bbb R}$ }[X,Y]$](img6.png) で
で
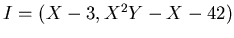 の場合。
の場合。
- 3.
-
![$R=\mbox{${\Bbb R}$ }[X,Y]$](img6.png) で
で
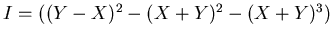 の場合。
の場合。
- 4.
-
![$R=\mbox{${\Bbb R}$ }[X,Y,Z]$](img9.png) で
で 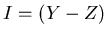 の場合。
の場合。
問題 1.1-1.4 のうちから2つを選び、解きなさい。
(解答)
(1) ![]() の
の
![]() での解の全体が答えになる。
での解の全体が答えになる。
(2) 連立方程式
![]()
の解を求めればよい。
答えは ![]() を平面上にプロットしたものである。
を平面上にプロットしたものである。
(3)
この問題はちと難しかったかも知れない。
![]() とおくと、
とおくと、
![]() に関する上の式は講義で扱ったから描けるはずである。
に関する上の式は講義で扱ったから描けるはずである。
![]() から
から ![]() に戻すには、単にこれを
に戻すには、単にこれを ![]() だけ回転させて
さらに
だけ回転させて
さらに ![]() 倍に縮小すればよい。
倍に縮小すればよい。
![\includegraphics[scale=0.5]{113.ps}](img24.png)
もちろん、「正攻法」で、![]() が大きい時等の漸近挙動等から総合的に判断して
グラフを描いてもよい。
が大きい時等の漸近挙動等から総合的に判断して
グラフを描いてもよい。
(解答)
(1)
![]() これは双曲線である。
これは双曲線である。
(2)
(3)
これは諸君の選んだ ![]() の取り方によるわけだが、
上の取り方ならば、
の取り方によるわけだが、
上の取り方ならば、
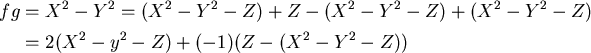
でたとえば ![]() とすればよい。
とすればよい。
(4)
![]() のなかでは、
のなかでは、
![]() ,
,
![]() がなりたっているわけであるから、
がなりたっているわけであるから、
(別のヒント:
![]() の間の関係式を求めるには、
実は3変数の多項式環
の間の関係式を求めるには、
実は3変数の多項式環
![]() のイデアル
のイデアル
![]() のグレブナ基底のうち、
のグレブナ基底のうち、![]() だけの多項式であるものを
取り出せばよいことが知られている。(辞書式順序について
だけの多項式であるものを
取り出せばよいことが知られている。(辞書式順序について
![]() である所がミソである)なぜこれでよいかは成書を見てもらうことにして、
とりあえずは計算してみると何をやっているか分かるかも知れない。)
である所がミソである)なぜこれでよいかは成書を見てもらうことにして、
とりあえずは計算してみると何をやっているか分かるかも知れない。)
(解答)
(1)
(2)
ヒントにあるように、
(3) (省略)
![]() のイデアル
のイデアル
![]() と
と
![]() とについて、
とについて、
![]() -準同型
-準同型
![]() を、
を、
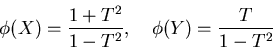
(解答)
この問題は問題11.2 とほぼ同じである。(もっと詳しく言えば、11.2 を単に
![]() 方向に
方向に ![]() に潰しただけである。)したがって解答は省略する。
に潰しただけである。)したがって解答は省略する。