


Next: About this document ...
代数学特論 II 要約 No.2
今日のテーマ:
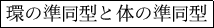
定義 2.1 (環に元を付け加えてできる
環)
環
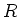
と、その部分環
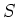
,
および
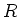
の元
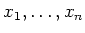
が
与えられているとする。
このとき、
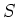
と
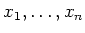
とを含む
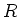
の部分環のうち最小のものを
![$S[x_1,\dots,x_n]$](img5.png)
(
角括弧に注意)
と書き、
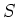
に
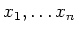
を付け加えてできる環と呼ぶ。
一般に、体 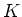 と、その部分体
と、その部分体 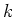 ,
および
,
および 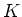 の元
の元
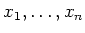 が
与えられていたとしても、
が
与えられていたとしても、
![$k[x_1,\dots,x_n]$](img9.png) は体とは限らない。
は体とは限らない。
定義 2.2 (体に元を付け加えてできる
体)
体
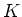
と、その部分体
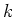
,
および
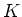
の元
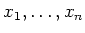
が
与えられているとする。
このとき、
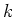
と
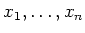
とを含む
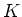
の部分体のうち最小のものを
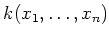
(
丸括弧に注意)
と書き、
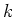
に
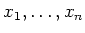
を付け加えてできる体と呼ぶ。
上の二つの定義では、すでに存在する
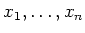 を
付け加えることを考えているが、
「変数」
を
付け加えることを考えているが、
「変数」
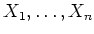 を付け加えたものもそれに準じて定義される。すなわち、
を付け加えたものもそれに準じて定義される。すなわち、
- 環
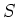 に対して、
に対して、
![$S[X_1,\dots,X_n]$](img12.png) (角括弧)は
(角括弧)は
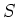 を係数にもつ
を係数にもつ 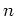 変数の多項式環であり、
変数の多項式環であり、
- 体
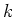 に対して、
に対して、
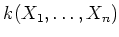 (丸括弧)は
(丸括弧)は
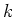 を係数にもつ
を係数にもつ 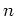 変数の有理関数体である。
変数の有理関数体である。
◆ 角括弧と丸括弧の使い分けは次のように覚えておくと良い。
環を作る→角括弧
体を作る→丸括弧
![${\Bbb C}[X]$](img16.png) と
と
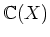 との違いがわかることが大事である。
との違いがわかることが大事である。
補題 2.1
整域
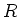
が与えられている時、形式的な「分数」の全体
の全体に同値関係を
でいれると、商集合
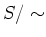
はおなじみの算法
によって体になる。
定義 2.3
上の
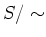
のことを
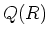
と書き、
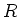
の全商体と呼ぶ。
補題 2.3
整域
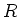
は体
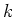
上環として有限生成であるとする。
すなわち、ある
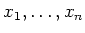
という
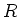
の有限個の元があって、
![$R=k[x_1,\dots,x_n]$](img25.png)
が成り立っているとする。
さらに、
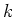
上の整域
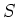
と、
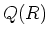
から
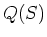
への
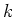
-準同型写像
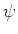
が与えられているとする。
このとき、ある
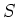
の元
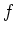
と環準同形写像
であって、
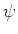
が
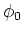
の拡張になっているものが存在する。
問題 2.1
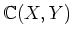
から
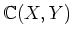
への準同形写像
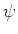
が、
で与えられているとする。(
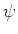
が体の準同型であることは
全く自明というわけでもないが、ここではそれは認めておくことにする。)
このとき、補題
2.3にあるような
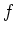
と
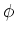
を求めよ。
問題 2.2
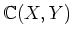
から
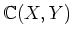
への準同形写像
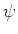
を、
で与えることはできない。これはなぜか答えなさい。
2001-10-02
![]()
![]() と、その部分体
と、その部分体 ![]() ,
および
,
および ![]() の元
の元
![]() が
与えられていたとしても、
が
与えられていたとしても、
![]() は体とは限らない。
は体とは限らない。
![]() を
付け加えることを考えているが、
「変数」
を
付け加えることを考えているが、
「変数」
![]() を付け加えたものもそれに準じて定義される。すなわち、
を付け加えたものもそれに準じて定義される。すなわち、
![]() と
と
![]() との違いがわかることが大事である。
との違いがわかることが大事である。