Next: About this document ...
代数学特論 II 要約 No.9
今日のテーマ:

補題 9.1
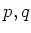
は複素数で、
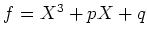
の判別式は
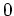
でないとする。
このとき、
![${\Bbb C}[X,Y]/(Y^2-X^3-pX-q)$](img5.png)
の商体を
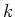
とすると、
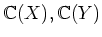
はともに
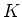
の部分体と見ることができて、
![$[K:{\Bbb C}(X)]=2$](img9.png)
,
![$[K:{\Bbb C}(Y)]=3$](img10.png)
がなりたつ。
判別式の定義は以下に述べる。
定義 9.1
を
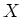
について展開して得られる多項式の係数のことを
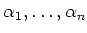
の基本対称式という。
補題 9.2
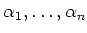
の対称式であるような多項式は
必ず
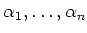
の基本対称式の多項式として表される。
補題 9.3
体
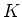
上の
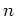
次多項式
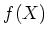
に対して、
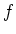
の根を
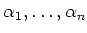
とし、
とおくと、
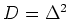
は
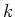
の元である。この
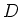
のことを
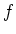
の
判別式と言う。
明らかに、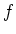 の判別式が
の判別式が 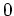 になることと
になることと 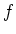 が重根を持つことは同値である。
が重根を持つことは同値である。
問題 9.1
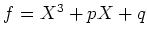
の判別式を具体的に
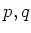
の多項式で表しなさい。
2002-01-06
![]()