今日のテーマ:
![]()
今回を通じて、
![]() ,
,
![]() (
(![]() -上の
-上の ![]() -変数
有理式のうちで、
-変数
有理式のうちで、
![]() の対称式であるもの全体)
とおく。
の対称式であるもの全体)
とおく。
定理10.1 で現れる
![]() の部分群
の部分群 ![]()
![]()
![]() による不変体
による不変体 ![]()
という対応は、じつは ![]() の部分群と、
の部分群と、![]() と
と ![]() の
中間体(
の
中間体(![]() の部分体で
の部分体で ![]() を含むもの) の間の一対一
対応を与えている。
この一般化がいわゆるガロア理論である。
この講義ではそこまで触れられなかったが、
定理10.1 の証明そのものは(4)を除きほぼ完結している。
ここではその証明の補遺になるものをいくつか問題としておく。
を含むもの) の間の一対一
対応を与えている。
この一般化がいわゆるガロア理論である。
この講義ではそこまで触れられなかったが、
定理10.1 の証明そのものは(4)を除きほぼ完結している。
ここではその証明の補遺になるものをいくつか問題としておく。
いま、 ![]() の部分群
の部分群 ![]() をとって、
さらに
をとって、
さらに
![]() を
を
![]() なるように選ぶと、
補題10.2 (と講義での注意)で証明した通り、
なるように選ぶと、
補題10.2 (と講義での注意)で証明した通り、
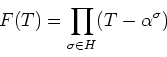
このことから、定理10.1 の(1),(2),(3)はすぐに従う。
このような ![]() の存在(補題10.3) を示すためには、
次のような問題を解けば良い。
の存在(補題10.3) を示すためには、
次のような問題を解けば良い。
定理10.1(4) を証明するのは今回の講義だけの知識では 少し足りない。どのような道筋で証明されるかは、 次の二つの問題の形式で出しておこう。解けなくても気にやむ必要はない。
最後に、次のような問題を出しておこう。解けば不変式の知識が深まるに違いない。