


Next: About this document ...
代数学II 要約 No.2
今日のテーマ:
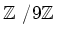 での計算は、九去法(あるいは、ナントカ占い)の名で知られている
ものの簡単な説明を与える。
での計算は、九去法(あるいは、ナントカ占い)の名で知られている
ものの簡単な説明を与える。
例題 2.1
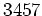
を
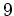
で割ったあまりを求めよ。
(解答)
![\begin{align*}&[3457]_9 \\
=&[3\times 10^3+4\times 10^2+5\times 10+7]_9\\
=&[3...
...^2+[5]_9\times [10]_9+[7]_9\\
=&[3]_9+[4]_9+[5]_9+[7]_9\\
=&[1]_9
\end{align*}](img5.png)
つまり
![$[10]_9=[1]_9$](img6.png) であることが最大のポイントなわけだ。
同様にして、10進法で書いた数を
であることが最大のポイントなわけだ。
同様にして、10進法で書いた数を 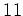 で割ったあまりも
簡単に求めることができる。(
で割ったあまりも
簡単に求めることができる。(
![$[10]_{11}=[-1]_{11}$](img8.png) )に注意)
)に注意)
環 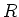 に対して、その単位元を
に対して、その単位元を 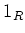 ,
と書き、
,
と書き、 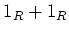 を
を 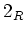 とかく。
とかく。
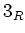 ,
,
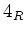 等も同様。(この
等も同様。(この 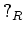 の
の 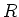 は「石井浩郎」と「石井琢郎」
を区別するのに
は「石井浩郎」と「石井琢郎」
を区別するのに
 とか
とか
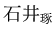 とかくのと同様で、言わなくても分かるときには省略する。)
とかくのと同様で、言わなくても分かるときには省略する。)
定義 2.1 (環の標数)
ある正の整数
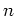
があって、
が成り立つとき、このような
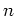
のなかで正で最小のものを
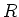
の標数と呼ぶ。
そのような
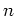
がないときには、
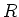
の標数は
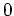
であると定義する。
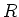
の標数のことを、以下では
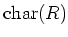
と書く。
例
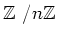
の標数は
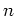
である。
上で、「余り」というものがでたついでに、整数同士の「余りを許した割り算」
について復習しておこう。この講義では特に断らない限りは次の意味の割り算をする。
定義 2.2
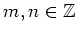
とし、
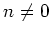
であるとする。このとき、
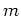
を
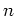
で割った商
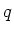
と、余り
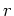
とは、次の関係式を満たす唯一のものとして定義される。
この定義では、 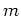 や
や 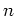 が負の数でも構わないということに注意しておく。
余りだけについて言えば、次のような言い換えも可能である。
が負の数でも構わないということに注意しておく。
余りだけについて言えば、次のような言い換えも可能である。
割り算を用いて次の結果を証明できる
補題 2.1
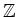
のイデアルは
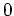
か、または
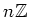
(
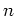
は正の整数)の形のものに限る。
前回、時間が余ったので次の補題について述べた
先週述べたこの補題の証明はもう少し一般化できる。
まず次の言葉を用意しておこう。
定義 2.3
- 1.
- 環
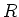 の元
の元 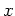 が零因子であるとは、ある
が零因子であるとは、ある 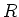 の元
の元 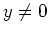 があって、
があって、
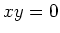 が成り立つときに言う。
が成り立つときに言う。
- 2.
- 環
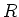 が
が 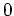 以外に零因子を持たないとき、
以外に零因子を持たないとき、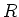 は整域であると言う。
は整域であると言う。
補題 2.3
- 1.
- 元の個数が有限の環の非零因子は必ず可逆である。
- 2.
- 元の個数が有限の環
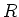 が整域ならば、
が整域ならば、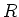 は体である。
は体である。
レポート問題が複数ある場合には、一つを選んで解くこと。
保険のために二つ選んでもよい。その場合には評価はよい方のものを与える。
(和にはならない。)
問題 2.1
10進法で書いた整数
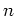
(例:
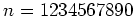
)
を13 で割った余りを求めるのは、
9や11のときほど簡単ではないが、つぎのようにできる。
- 1.
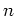 を三桁毎に区切る。(
を三桁毎に区切る。(
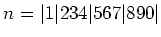 )
)
- 2.
- 区切ったものをそれぞれ符号をつけて加える。
- 3.
- 加えた答えを
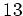 で割った余りを求める。
(
で割った余りを求める。
(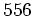 を
を 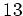 で割った余りは
で割った余りは 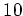 )
)
この最後の答えが
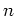
を
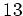
で割った答えである。これはなぜか説明せよ。
問題 2.2
上と同様な考察により、
10進法で書いた整数を
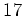
で割った余りを「一定の桁数毎に区切って」
求める方法はないか?
問題 2.3
一般に、素数
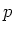
に対して、
10進法で書いた整数を
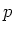
で割った余りを「一定の桁数毎に区切って」
求める方法はいつでも存在するだろうか?
(但しもちろん
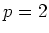
と
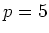
の場合は例外とする。)
2002-04-18
![]()
![]() での計算は、九去法(あるいは、ナントカ占い)の名で知られている
ものの簡単な説明を与える。
での計算は、九去法(あるいは、ナントカ占い)の名で知られている
ものの簡単な説明を与える。
![\begin{align*}&[3457]_9 \\
=&[3\times 10^3+4\times 10^2+5\times 10+7]_9\\
=&[3...
...^2+[5]_9\times [10]_9+[7]_9\\
=&[3]_9+[4]_9+[5]_9+[7]_9\\
=&[1]_9
\end{align*}](img5.png)
![]() であることが最大のポイントなわけだ。
同様にして、10進法で書いた数を
であることが最大のポイントなわけだ。
同様にして、10進法で書いた数を ![]() で割ったあまりも
簡単に求めることができる。(
で割ったあまりも
簡単に求めることができる。(
![]() )に注意)
)に注意)
![]() に対して、その単位元を
に対して、その単位元を ![]() ,
と書き、
,
と書き、 ![]() を
を ![]() とかく。
とかく。
![]() ,
,
![]() 等も同様。(この
等も同様。(この ![]() の
の ![]() は「石井浩郎」と「石井琢郎」
を区別するのに
は「石井浩郎」と「石井琢郎」
を区別するのに
![]() とか
とか
![]() とかくのと同様で、言わなくても分かるときには省略する。)
とかくのと同様で、言わなくても分かるときには省略する。)