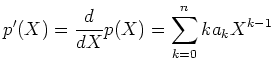: この文書について...
代数学II 要約 No.7
今日のテーマ:

前回、いくつかの定理と補題の証明が残ってしまっていた。
定理 7.1 (定理6.1と同じ)
素数
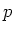
と正の整数
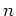
にたいして、 元の数が
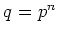
の体は存在する。
もっと詳しくいうと、
![% latex2html id marker 767
$ X^q-X \in F_p[X]$](img5.png)
が一次式の積に分解するような体
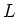
(前の補題によって存在する) をとり、
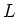
のなかの
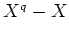
の根の全体を
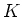
とおくと、
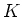
は体で、その元の数は
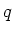
になる。
この定理のうち、 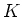 が体で、その元の数が
が体で、その元の数が 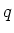 以下であることは前回
証明した。
以下であることは前回
証明した。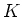 の元の数がちょうど
の元の数がちょうど 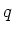 個であることを示すには、
多項式の微分の概念を知っておいた方が便利である。
個であることを示すには、
多項式の微分の概念を知っておいた方が便利である。
補題 7.1
体
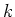
上の多項式
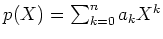
に対して、
その微分を
で定義する。この時、
- 微分は
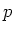 の係数体をどう選ぶかに関係しない。
の係数体をどう選ぶかに関係しない。
- 微分は
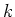 -線型である。
-線型である。
-
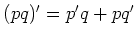 .
.
定理 7.2 (定理6.2とおなじ)
有限体
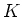
にたいして、位数が
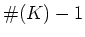
であるような
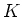
の元
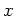
が存在する。
言い換えると、
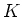
の乗法群
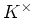
は巡回群である。
系 7.1
素数
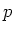
と正の整数
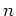
に対して、
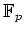
上の既約多項式
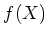
で、
その次数が
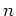
のものが存在する。
注意:次の問題は(いつもの例に反して)難易度の順に並んでいない.
解きやすいものをとくこと。
また、これらは本質的に違う問題というわけではないので、今回は
一問のみを選んで解くこと。
問題 7.1
元の数が
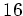
の体
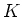
を
![$ {\mathbb{F}}_2[X]/f(X){\mathbb{F}}_2(X)$](img28.png)
の形でつくり、
その
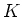
に対して
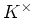
の生成元を一つ求めなさい。
問題 7.2
元の数が
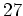
の体
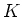
を
![$ {\mathbb{F}}_3[X]/f(X){\mathbb{F}}_3(X)$](img30.png)
の形でつくり、
その
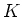
に対して
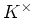
の生成元を一つ求めなさい。
問題 7.3
元の数が
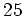
の体
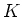
を
![$ {\mathbb{F}}_5[X]/f(X){\mathbb{F}}_5(X)$](img32.png)
の形でつくり、
その
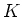
に対して
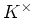
の生成元を一つ求めなさい。
2002年6月4日
![]()
![]() が体で、その元の数が
が体で、その元の数が ![]() 以下であることは前回
証明した。
以下であることは前回
証明した。![]() の元の数がちょうど
の元の数がちょうど ![]() 個であることを示すには、
多項式の微分の概念を知っておいた方が便利である。
個であることを示すには、
多項式の微分の概念を知っておいた方が便利である。