今日のテーマ:
![]()
以下 ![]() は素数であるとし、
は素数であるとし、![]() (
(![]() は正の整数)であるとする。
は正の整数)であるとする。
方程式系
![]() 個の変数
個の変数
![]() に関する
に関する
![]() 係数の多項式
係数の多項式
![]() が与えられているとき、
方程式系
が与えられているとき、
方程式系
![]() での
での
![]() の解の全体を
の解の全体を
![]() で書き表す。
で書き表す。
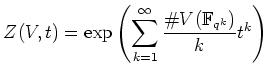
上の定義は幾分わかりにくいかも知れない。この式の ![]() は
実は結果を有理式にするための工夫である。
いま、
は
実は結果を有理式にするための工夫である。
いま、
![]() となるような行列
となるような行列 ![]() が
存在したとするならば、
が
存在したとするならば、
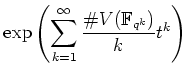 |
||
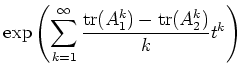 |
||
と行列式表示ができる。このような ![]() があるかどうか、
その固有値はどのようなものであるか、が面白い所であるが、本講義では
さすがにそこまでは踏み込めない。
があるかどうか、
その固有値はどのようなものであるか、が面白い所であるが、本講義では
さすがにそこまでは踏み込めない。
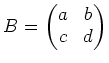 の階数を
の階数を