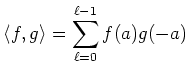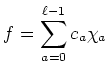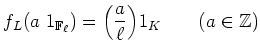: この文書について...
代数学II 要約 No.13
今日のテーマ:

前回、平方剰余の相互法則の証明が残ってしまっていた。
ガウスの和の定義の復習から書いておこう。
定義 13.1
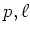
は相異なる奇素数であるとし、
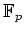
の拡大体の
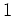
の原始
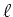
-乗根
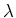
を取る。
整数
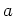
に対して、有限体のガウス和
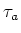
を
で定義する。
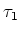
のことを単に
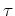
とかく。
ついでにこの定義の意味についてもう少しだけ述べておこう。
まず、上の 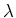 は次のようにしてとることができる。
は次のようにしてとることができる。
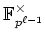 は位数
は位数
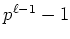 の巡回群で、
その生成元を
の巡回群で、
その生成元を 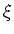 とおく。
フェルマーの小定理により
とおく。
フェルマーの小定理により
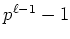 は
は 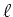 で割り切れるから、
で割り切れるから、
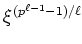 を考えることができる。この元の
位数はちょうど
を考えることができる。この元の
位数はちょうど 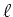 であるから、これを
であるから、これを 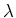 とすればいい。
なお、
とすればいい。
なお、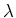 の取り方は一意的ではなく、
1の
の取り方は一意的ではなく、
1の 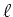 乗根は
乗根は 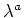
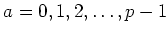 の
の 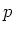 個ある。
これらに対応して
個ある。
これらに対応して 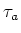 ができる。下の補題の(1)はそれらが符号の差を除いて
等しいことを述べている。ただし、
ができる。下の補題の(1)はそれらが符号の差を除いて
等しいことを述べている。ただし、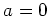 のときだけは
特別で、
のときだけは
特別で、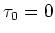 がなりたつ。
がなりたつ。
定理 13.1 (平方剰余の相互法則)
奇素数
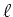
に対して次の等式が成り立つ。
-
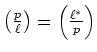 (但し
(但し
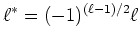 )
)
問題 13.1
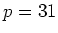
,
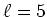
にたいして、
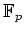
の
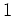
の原始
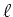
-乗根を
一つ見つけ、ガウスの和
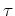
を求めて、
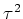
を実際に計算してみなさい。
問題 13.2
奇素数
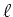
と、体
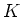
が与えられていて、
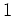
の原始
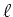
乗根
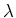
が
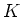
のなかに存在するとする。
(とくに、
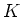
の標数は
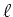
ではない。)
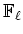
上の
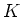
-値関数の全体
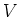
は (各点ごとの加法、スカラー倍により)
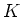
上のベクトル空間になり、
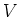
上に内積が
で定まる。(証明不要)
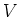 の
の 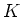 上の次元を求めよ。(答のみでよい。)
上の次元を求めよ。(答のみでよい。)
- (指標の直交性。)
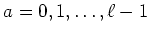 に対して、
に対して、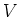 の元
の元 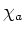 を、
で定義するとき、内積
を、
で定義するとき、内積
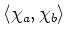 を求めよ。
を求めよ。
-
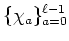 は
は 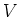 の基底であることを示しなさい。
さらに、
の基底であることを示しなさい。
さらに、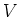 の元
の元 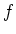 を
と書くためには、
を
と書くためには、 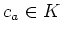 をどのように求めればよいか、述べなさい。
をどのように求めればよいか、述べなさい。
問題 13.3
前問と同じ仮定の下で、
フーリエ変換
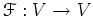
を、
で定義する。このとき、
-
![$ \langle \mathcal F[f],\chi_a\rangle =\ell f(-a)$](img46.png) がなりたつこと
を示しなさい。
がなりたつこと
を示しなさい。
-
![$ \mathcal F[\mathcal F[f]]$](img47.png) を計算し、
を計算し、
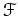 の逆変換を求めなさい。
の逆変換を求めなさい。
- 任意の
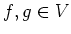 に対して、
に対して、
![$ \langle \mathcal F[f],g \rangle=\langle f,\mathcal F [g]\rangle$](img50.png) が
成り立つことを示しなさい。
が
成り立つことを示しなさい。
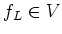 を
で定義する。
を
で定義する。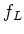 は
は
 の固有ベクトルであることを示し、
それが属する固有値を求めなさい。
の固有ベクトルであることを示し、
それが属する固有値を求めなさい。
2002年7月15日
![]()
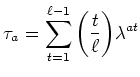
![]() は次のようにしてとることができる。
は次のようにしてとることができる。
![]() は位数
は位数
![]() の巡回群で、
その生成元を
の巡回群で、
その生成元を ![]() とおく。
フェルマーの小定理により
とおく。
フェルマーの小定理により
![]() は
は ![]() で割り切れるから、
で割り切れるから、
![]() を考えることができる。この元の
位数はちょうど
を考えることができる。この元の
位数はちょうど ![]() であるから、これを
であるから、これを ![]() とすればいい。
なお、
とすればいい。
なお、![]() の取り方は一意的ではなく、
1の
の取り方は一意的ではなく、
1の ![]() 乗根は
乗根は ![]()
![]() の
の ![]() 個ある。
これらに対応して
個ある。
これらに対応して ![]() ができる。下の補題の(1)はそれらが符号の差を除いて
等しいことを述べている。ただし、
ができる。下の補題の(1)はそれらが符号の差を除いて
等しいことを述べている。ただし、![]() のときだけは
特別で、
のときだけは
特別で、![]() がなりたつ。
がなりたつ。
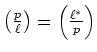 (但し
(但し