(答え)
![]() で、
で、![]() が
が ![]() で割り切れればよい。
で割り切れればよい。
(証明)
便宜上, 最初の写像を ![]() ,次の写像を
,次の写像を ![]() とおく。
とおく。
![]() なら
なら ![]() となるのは不可能なので、
となるのは不可能なので、 ![]() の場合を考える。
このとき、
の場合を考える。
このとき、
![]() であるから,
であるから,
![]() のときの
のときの
![]() と
と ![]() の値が一致するかどうか調べればよい。
の値が一致するかどうか調べればよい。
いま、
![]() なる整数
なる整数 ![]() があったとすると、
フェルマの小定理により
があったとすると、
フェルマの小定理により
逆に, ![]() と仮定しよう。
と仮定しよう。![]() を
を ![]() で割った
商を
で割った
商を ![]() , あまりを
, あまりを ![]() とおくと、全ての
とおくと、全ての
![]() にたいして,
にたいして,
この問題に限らず、解答は証明(とは言わないまでもなぜその答えで正しいかの 説明)があってはじめて一人前である。
(答え)
これは簡単である。標数 0 なら
![]() で
で
標数が正のものに関しては、標数 ![]() の
の
![]() で
で
標数 ![]() の
の
![]() で,
で,
などを反例にあげればよい。
(答え)
この問題はまちがっておった。二次式のほうは ![]() にすべきであった。
にすべきであった。
![]() は既約でないからである。
は既約でないからである。
問題のままでは, ![]() は一次式の積に分解できない。
ただし(なぜ分解できないかまで含めた)正しい指摘は皆無であった。寂しい限りである。
は一次式の積に分解できない。
ただし(なぜ分解できないかまで含めた)正しい指摘は皆無であった。寂しい限りである。
本当は
![]() の位数が 24 であることを用いる問題だった。
の位数が 24 であることを用いる問題だった。
![]() と
と ![]() の共通部分は
の共通部分は
![]() の二点である。
それ以外は講義で説明した通りである。
念のために述べておくと、
の二点である。
それ以外は講義で説明した通りである。
念のために述べておくと、
![]() とおいて,
とおいて,
![]() の元の
数を求める必要があるのだが、
の元の
数を求める必要があるのだが、
(1) ![]() が
が
![]() で平方根を持つときには、
で平方根を持つときには、
![]() の元の数は
の元の数は
![]() の元の数と同じであって、
の元の数と同じであって、![]() である。
である。
(2) ![]() が
が
![]() で平方根を持たないときには,
で平方根を持たないときには,
![]() の元のうち
の元のうち ![]() 以外は
以外は
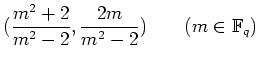
したがって ![]() が modulo
が modulo ![]() で平方剰余ならば,
で平方剰余ならば,
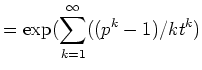 |
||
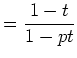 |
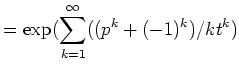 |
||
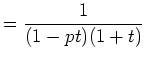 |
あとは、一般に,方程式系 ![]() に対して,
に対して,
答えは
![]() が平方剰余のとき(つまり
が平方剰余のとき(つまり ![]() を
を ![]() で割ったあまりが
で割ったあまりが ![]() または
または ![]() のとき,
のとき,
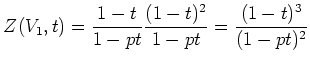
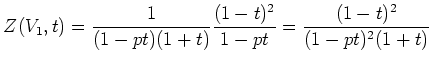
![]() 座標
座標 ![]() の値によって
の値によって
![]() の元を分類すればよい。
(これは幾何学的には円錐を平面で切ることにあたる).
の元を分類すればよい。
(これは幾何学的には円錐を平面で切ることにあたる).
![]() のときは、
のときは、
![]() の解の数だが、これは先刻承知(
の解の数だが、これは先刻承知(![]() )のはずである。
)のはずである。
![]() のときは、
のときは、![]() ,
, ![]() を
を ![]() と変数変換することにより,
と変数変換することにより,
![]() をえる。
この解の数は前問同様
をえる。
この解の数は前問同様 ![]() になる。あとはそれらを足せばよい。
になる。あとはそれらを足せばよい。
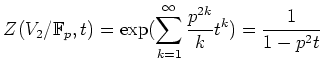
(答え)
MuPAD の powermod 関数をつかえば簡単であった。答えは ![]() である。
したがって、フェルマの小定理の対偶により,
である。
したがって、フェルマの小定理の対偶により, ![]() は素数でないことがわかる。
念のためにいっておくと,
は素数でないことがわかる。
念のためにいっておくと, ![]() だからと言って、
だからと言って、![]() が
素数であるとは限らない。
が
素数であるとは限らない。
powermod なんぞ知らぬという人のほうが多いであろう。 次の等式を何度も使えばよい。
いずれにせよ、計算機を活用しないと面倒な問題であった。