代数学特論II 要約 No.3

今日のテーマ:

前回の流れから行くと、行列 $A$ をまず弱固有空間ごとに分けて考えて、 それぞれの部分で $A$ の標準型を考えるのが自然であるのだが、 若干見方をかえて加群の理論から話を進めよう。 $n$ 次正方行列 $A \in M_n({\mathbb{C}})$ が与えられているとする。$A$ は

$$V={\mathbb{C}}^n ={\mathbb{C}}e_1+{\mathbb{C}}e_2 + {\mathbb{C}}e_3+\dots {\mathbb{C}}e_n$$

に作用する。但し、ここに、$e_i$ は基本ベクトルである。$V$ には、多項式環 ${\mathbb{C}}[X]$ が、

$$X. v= A v \qquad ($$ 一般に $$p(X). v =p(A) v)$$

(右辺は行列とベクトルのかけ算)として作用している。ドット (.) に注意。 作用を考えるときにはいつでもこのドットをつける。

さて、$V$ の成分を多項式に拡張して、

$$F_0={\mathbb{C}}[X]^n =\left\{ \begi... ..._n(X) \end{pmatrix} ; a_i (X)\in {\mathbb{C}}[X] \quad(i=1,2,\dots,n) \right\}$$

というのを考えよう。$F_0$ の元 ${}^t(a_1(X),a_2(X),\dots,a_n(X))$ というのは 形式的に

$$\begin{pmatrix} a_1(X)\\ a_2(X)\\ a_3(X)\\ \vdots\\ a_n(X) \end{pmatrix} =a_1(X) e_1 +a_2(X) e_2+a_3(X) e_3+ \dots + a_n(X)e_n$$

と書くこともできる。こっちのほうはドットがつかないことに注意。 ドットや、行列の積との区別を強調するために、こちらのほうのことを

$$\begin{pmatrix} a_1(X)\\ a_2(X)\\ a_3(X)\\ \vdots\\ a_n(X) \e... ...(X)\otimes e_1 +a_2(X)\otimes e_2+a_3(X)\otimes e_3+ \dots + a_n(X)\otimes e_n$$

と書くこともある。($\otimes$ はテンソル記号と呼ばれる。)

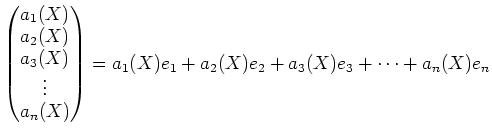
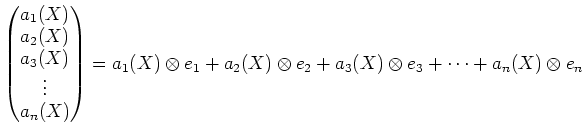
テンソル記号をドットに置き換える操作を $\phi$ と書こう。 すなわち、 $\phi: F_0 \to V$ を

$$\phi (a_1(X) \otimes e_1+ a_2(X) \otimes e_2+ a_3(X)\otimes e_3 +\dots+ a_n(X)\otimes e_n)$$

$$= a_1(X). e_1+ a_2(X) . e_2+ a_3(X). e_3 +\dots+ a_n(X). e_n$$

$$= a_1(A) e_1+ a_2(A) e_2+ a_3(A) e_3 +\dots+ a_n(A) e_n$$

で定義する。

$\phi$ は線型写像で、全射であることはすぐに分かる。 $\phi$ の核は、次のような線型写像の像と一致する。

$$\psi: F_1={\mathbb{C}}[X]^n \ni L \mapsto (X E -A) L\in {\mathbb{C}}[X]^n=F_0$$

$\psi$ を $F_1$ と $F_0$ の基底を取り換えることによって、できるだけ やさしい表示にすること、これがポイントである。 実は、 $X E-A$ のような特殊な元に限らず、そのようなやさしい表示がある。

すなわち、 ${\mathbb{C}}[X]$ ではユークリッド除法（余りを許した割り算)ができることから、 「掃き出し法」が使えて、次のような命題が成り立つ。

命題 3.1   $M_n({\mathbb{C}}[X])$ の元 $B$ に対して、 ${\mathbb{C}}[X]$ の元を成分にもつ行列 $P,Q$ で、 $\operatorname{det}(P)=1,\operatorname{det}(Q)=1$ を満たし、

$$P B Q= \begin{pmatrix} d_1(X) \\ & d_2 (X) \\ & & d_3(X) \\ & ... ... \\ & & & & & & 0 \\ & & & & & & & \ddots \\ & & & & & & & & 0 \end{pmatrix}$$

(ただし $d_1(X) \vert d_2(X) \vert d_3(X) \vert\dots \vert d_s(X)$) という形にできるものが存在する。

上の $d_1(X) ,d_2(X), d_3(X) ,\dots , d_s(X)$ は $B$ の単因子と呼ばれる。

上の $P,Q$ はそれぞれ 次のような「基本変形」を具体的に表現するような行列の積である。

1. $P$ ...(行変形) $B$ のある行の多項式倍を $B$ の別の行に加える。
2. $Q$ ...(列変形) $B$ のある列の多項式倍を $B$ の別の列に加える。

この続きは次回にまわす。

問題 3.1   ${\mathbb{C}}[X]$ の元を成分にもつ $3$ 次の正方行列

$$B= \begin{pmatrix} X & 1 & 0 \\ 0 & X^2 & 1 \\ 0 & 0& X^3 \end{pmatrix}$$

に対して、命題 3.1を満たす $d_1,d_2,\dots,d_r$ および $P,Q$ を具体的に求めなさい。