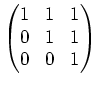: この文書について...
代数学特論II 要約 No.4
今日のテーマ:

先週に引き続き、
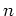 次正方行列
次正方行列
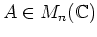 が与えられているとする。
が与えられているとする。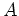 は
は
に作用する。前回やったように、次のような 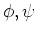 がある。
但し、
がある。
但し、 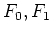 はモノとしては同じで、
である。
はモノとしては同じで、
である。
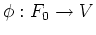 は
は
で、 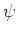 は
で定義されるような写像であった。
は
で定義されるような写像であった。
これは、次のような問題を解いていることに当たる。
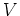 の各元は複素数倍と和を用いて
の各元は複素数倍と和を用いて
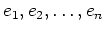 でうまく表示できたが、
でうまく表示できたが、
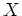 も一緒に用いるとどのぐらいうまく表示できるだろうか。
も一緒に用いるとどのぐらいうまく表示できるだろうか。
先週の単因子をもちいると、次のような単純な解答がある
定理 4.1
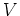
は
![$ {\mathbb{C}}[X]$](img21.png)
-加群として
![$ {\mathbb{C}}[X]/d(X){\mathbb{C}}[X]$](img22.png)
の形の加群の
直和と同型である。
とくに、巾零行列の表現空間は、
![$ {\mathbb{C}}[X]/X^k {\mathbb{C}}[X]$](img23.png) の形の加群の
直和に分解される。
の形の加群の
直和に分解される。
この定理を行列の言葉で書くとジョルダンの標準型が得られる。
例を挙げよう。
とする。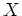 の
の
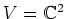 への作用を
への作用を 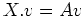 で定めると、
これは次のような行列算で表現できる。
で定めると、
これは次のような行列算で表現できる。
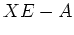 を前回やったように
と書いてみる。ただし
である。すると、
を前回やったように
と書いてみる。ただし
である。すると、
![$ {\mathbb{C}}[X]$](img21.png) -加群としては
-加群としては 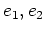 のかわりに
の第一、第二成分である
のかわりに
の第一、第二成分である 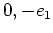 を用いるのが便利だということになる。
すなわち、
を用いるのが便利だということになる。
すなわち、
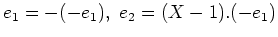 が成り立つ
ということにも注意しておこう。
が成り立つ
ということにも注意しておこう。
関数の設計。
No2.のレポート問題は少し難しかったようである。問題は、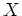 の関数
の関数 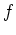 で、
次のような性質をもつものをつくりだすところにある。
で、
次のような性質をもつものをつくりだすところにある。
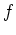 は
は 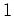 で 零点をもつ。
すなわち、
で 零点をもつ。
すなわち、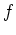 は
は 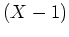 で割り切れる。
で割り切れる。
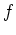 は、
は、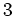 で三重の零点をもつ、
すなわち、
で三重の零点をもつ、
すなわち、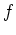 は
は 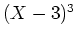 で割り切れる。
で割り切れる。
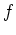 は、
は、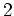 で 二重の「
で 二重の「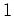 」点をもつ、
すなわち、
」点をもつ、
すなわち、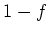 は
は 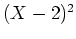 で割り切れる。
で割り切れる。
(同様のものを3つ作る必要がある。)
(ア)もっとも手軽な方法は、次のようにすることであろう。
- Step 1..
-
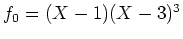 を考える。 (
を考える。 (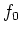 は上の (1),(2)の条件を満たす。)
は上の (1),(2)の条件を満たす。)
- Step 2..
-
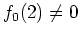 なので、
なので、
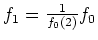 とおく。
(これで
とおく。
(これで 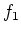 は 上の条件を満たすうえ、
は 上の条件を満たすうえ、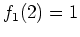 をも満たしている。
をも満たしている。
- Step 3..
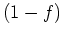 は
は 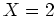 で零点をもつが、二重の零点をもつような関数を
作るには
で零点をもつが、二重の零点をもつような関数を
作るには 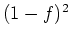 と、それを二乗してやればよいことに注意する。
と、それを二乗してやればよいことに注意する。
- Step 4..
-
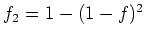 を考えれば、これは上の条件(1),(2),(3)を全て満たしている。
を考えれば、これは上の条件(1),(2),(3)を全て満たしている。
この方法は、求める関数が確かに存在することを保証するには明解で便利であるが、
次数が若干高くなるのが欠点である。 そこで、
(イ)
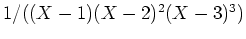 を部分分数展開する方法もある。
を部分分数展開する方法もある。
とやって、
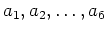 を(留数その他の方法で)求めて、
そこから
を(留数その他の方法で)求めて、
そこから 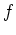 を計算するのである。例えば
を計算するのである。例えば 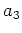 を研究するには
両辺に
を研究するには
両辺に 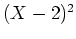 を掛けてから
を掛けてから 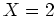 を代入すれば
(あるいは、
を代入すれば
(あるいは、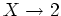 の極限をとれば)よい。
の極限をとれば)よい。
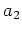 は 両辺に
は 両辺に 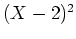 を掛けたあと一度
を掛けたあと一度 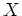 で微分して、
それから
で微分して、
それから 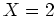 を代入することでもとめられる。
を代入することでもとめられる。
(ウ) 前回の講義の最後にやったように、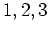 でそれぞれ
でそれぞれ 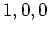 ,
, 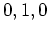 ,
, 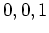 という値をとるような多項式
という値をとるような多項式
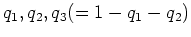 をとり、
をとり、
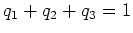 の両辺の高い巾を計算する。すなわち、
の両辺の高い巾を計算する。すなわち、
を考えるという手もある。左辺を展開して出てくる項は
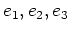 のどれか一つは大きくなるので、
のどれか一つは大きくなるので、
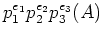 は
は
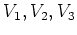 の
いずれかのみで 0 と異なる値をとる。これをもとに求める多項式を
計算するというわけである。
の
いずれかのみで 0 と異なる値をとる。これをもとに求める多項式を
計算するというわけである。
問題 4.1
次の行列のジョルダンの標準型を求めなさい。



: この文書について...
平成15年11月8日
![]()
![]() 次正方行列
次正方行列
![]() が与えられているとする。
が与えられているとする。![]() は
は
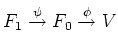
![% latex2html id marker 924
$\displaystyle F_0=F_1={\mathbb{C}}[X]^n
=\left\{
\...
..._n(X)
\end{pmatrix} ; a_i (X)\in {\mathbb{C}}[X] \quad(i=1,2,\dots,n)
\right\}
$](img9.png)
![]() の各元は複素数倍と和を用いて
の各元は複素数倍と和を用いて
![]() でうまく表示できたが、
でうまく表示できたが、
![]() も一緒に用いるとどのぐらいうまく表示できるだろうか。
も一緒に用いるとどのぐらいうまく表示できるだろうか。
![]() の形の加群の
直和に分解される。
の形の加群の
直和に分解される。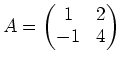
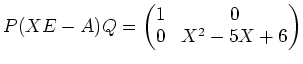
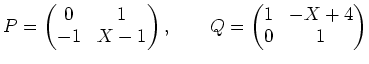
![]() の関数
の関数 ![]() で、
次のような性質をもつものをつくりだすところにある。
で、
次のような性質をもつものをつくりだすところにある。
![]() を部分分数展開する方法もある。
を部分分数展開する方法もある。
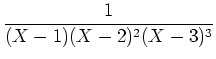
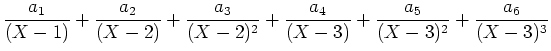
![]() でそれぞれ
でそれぞれ ![]() ,
, ![]() ,
, ![]() という値をとるような多項式
という値をとるような多項式
![]() をとり、
をとり、
![]() の両辺の高い巾を計算する。すなわち、
の両辺の高い巾を計算する。すなわち、