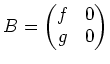: この文書について...
代数学特論II 要約 No.5
今日のテーマ:

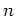 次正方行列
次正方行列
 が与えられているとする。
が与えられているとする。 は
は
に作用し、
![$ {\mathbb{C}}[X]$](img6.png) の
の 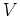 への作用を
で定義することができる。
和とスカラー倍に併せて、
への作用を
で定義することができる。
和とスカラー倍に併せて、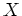 による作用も考えると、
(単因子の考え方を用いて)
による作用も考えると、
(単因子の考え方を用いて) 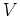 の生成元と
関係式を簡単化することができる。
の生成元と
関係式を簡単化することができる。
定理 5.1 (定理4.1 を再掲)
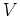
は
![$ {\mathbb{C}}[X]$](img6.png)
-加群として
![$ {\mathbb{C}}[X]/d(X){\mathbb{C}}[X]$](img10.png)
の形の加群の
直和と同型である。
とくに、巾零行列の表現空間は、
![$ {\mathbb{C}}[X]/X^k {\mathbb{C}}[X]$](img11.png) の形の加群の
直和に分解される。
の形の加群の
直和に分解される。
単因子の計算法は、第3回に述べたが、その時には比較的単純な
行列しか例に挙げなかった。本当は事情はもう少し複雑である。
(ユークリッドの互除法が必要になる。)
レポート問題を参照のこと。
![$ {\mathbb{C}}[X]/d(X){\mathbb{C}}[X]$](img10.png) の部分が気になるかも知れない。
この部分は(先週の関数の設計のところにも書いた)
の部分が気になるかも知れない。
この部分は(先週の関数の設計のところにも書いた) 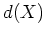 の
根による関数の分解をうまく用いる。
の
根による関数の分解をうまく用いる。
命題 5.2
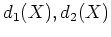
は互いに素な
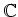
上の多項式であるとする。
このとき、
![$ {\mathbb{C}}[X]$](img6.png)
-加群としての同型
が存在する。(但し右辺への
![$ {\mathbb{C}}[X]$](img6.png)
の作用は対角型
で定まっているものとする。)
定理 5.3 (行列のジョルダンの標準型)
任意の行列
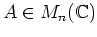
に対して、ある正則行列
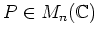
があって、
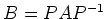
は
次のような形の行列(ジョルダンブロックと呼ばれる)の
直和(対角に並んだ形)に等しくなる。
ここに、
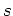
は
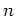
以下の整数、
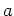
は複素数(
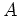
の固有値の一つ)である。
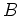
を
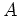
のジョルダンの標準型という
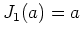
であることにも注意しておこう。
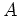
が対角化可能ならば、
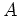
を対角化したものが
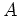
のジョルダンの標準型である。
ジョルダンブロックの形の行列は
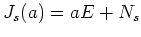 (
(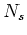 は巾零行列)の
形をしていることにも、特に注意しておこう。
とくに、任意の多項式
は巾零行列)の
形をしていることにも、特に注意しておこう。
とくに、任意の多項式 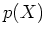 にたいして、
にたいして、
がなりたつ。とくに、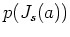 は
は 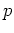 の
の 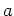 での
での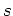 階までの微分の値
により完全に決まる。
階までの微分の値
により完全に決まる。
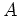 のほうで言えば、
のほうで言えば、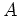 の固有値全体の集合を
の固有値全体の集合を 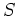 とおけば、
とおけば、
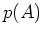 は
は 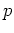 の
の 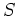 での(多く見積もっても
での(多く見積もっても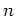 階までの)各階の導関数の値
によって完全に決まってしまう。
階までの)各階の導関数の値
によって完全に決まってしまう。
これは行列を 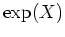 や
や 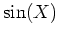 などの整関数
(全複素平面で正則な関数)や
もっと一般に
などの整関数
(全複素平面で正則な関数)や
もっと一般に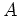 の固有値の近傍で正則な関数に代入するときのヒントになる。
の固有値の近傍で正則な関数に代入するときのヒントになる。
問題 5.1
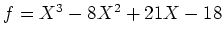
,
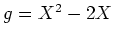
のとき、
にたいして命題 3.1 を満たす
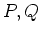
および
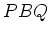
を求めなさい。
平成15年11月4日
![]()
![]() 次正方行列
次正方行列
![]() が与えられているとする。
が与えられているとする。![]() は
は
![]() の形の加群の
直和に分解される。
の形の加群の
直和に分解される。![]() の部分が気になるかも知れない。
この部分は(先週の関数の設計のところにも書いた)
の部分が気になるかも知れない。
この部分は(先週の関数の設計のところにも書いた) ![]() の
根による関数の分解をうまく用いる。
の
根による関数の分解をうまく用いる。
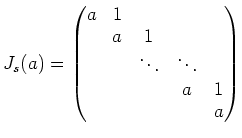
![]() (
(![]() は巾零行列)の
形をしていることにも、特に注意しておこう。
とくに、任意の多項式
は巾零行列)の
形をしていることにも、特に注意しておこう。
とくに、任意の多項式 ![]() にたいして、
にたいして、
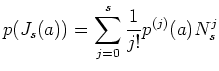
![]() や
や ![]() などの整関数
(全複素平面で正則な関数)や
もっと一般に
などの整関数
(全複素平面で正則な関数)や
もっと一般に![]() の固有値の近傍で正則な関数に代入するときのヒントになる。
の固有値の近傍で正則な関数に代入するときのヒントになる。