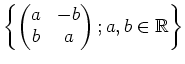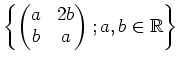: この文書について...
代数学特論II 要約 No.7
今日のテーマ:

定義 7.1
環
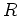
にあらたな元
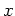
を付け加えてできた環を
![$ R[x]$](img4.png)
と書く。
付け加えるとはどういう意味だろうか。
大きく分けて二つの場合が考えられる。
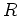 が大きな環
が大きな環 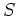 の部分環で、
の部分環で、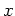 は
は 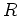 の元である場合。
の元である場合。
- とにかく抽象的な元
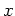 を考えて、それが
を考えて、それが 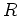 上適当な関係式を
満たすとして付け加える場合。
上適当な関係式を
満たすとして付け加える場合。
前者の場合には、「![$ R[x]$](img4.png) は、
は、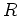 の元と、
の元と、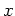 とを
加減乗除によってうまく組み合わせて作ったものの全体のなす環」
と考えればよい。
後者の場合には、具体的に
とを
加減乗除によってうまく組み合わせて作ったものの全体のなす環」
と考えればよい。
後者の場合には、具体的に ![$ R[x]$](img4.png) を構成する必要がある。(
この場合には、
を構成する必要がある。(
この場合には、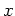 の関係式を別途記述する必要があるため、
の関係式を別途記述する必要があるため、
![$ R[x]$](img4.png) という記号だけでは
通常不十分である。)
という記号だけでは
通常不十分である。)
補題 7.1
モニックな
![$ R[X]$](img6.png)
の元
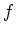
に対して、
![$ R_1=R[X]/f(X)R[X]$](img8.png)
は環になり、
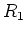
は
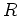
に
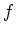
の根を一つ付け加えたもの
になっている。
補題 7.2
モニックな
![$ R[X]$](img6.png)
の元
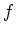
に対して、
![$ R_1=R[X]/f(X)R[X]$](img8.png)
を
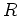
上の行列環の部分環として実現することができる。
具体的な環に具体的な元を付け加えるような場合でも、一旦上のテクニックを
駆使することにより、環の理解を増すことができる場合がある。
例 7.1
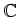
のなかで、
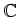
自身は
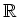
に
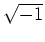
を付け加えた環と
考えることができるが、これは
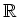
![$ [X]/(X^2+1)$](img13.png)
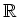
![$ [X]$](img14.png)
とも、
とも環としては同じ(同型)である。
例 7.2
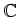
のなかで、
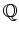
に
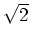
を付け加えた環
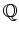
![% latex2html id marker 891
$ [\sqrt{2}]$](img18.png)
を
考えることができる。これは
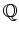
![$ [X]/(X^2-2)$](img19.png)
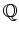
![$ [X]$](img14.png)
とも、
とも環としては同じ(同型)である。
命題 7.1
体
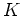
上のモニックな多項式
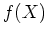
が
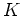
上既約ならば、
![$ K[X]/f(X) K[X]$](img23.png)
は体になる。逆も成り立つ。
問題 7.1
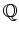
![% latex2html id marker 911
$ [\sqrt[3]{2}]$](img24.png)
を行列環の部分環として実現せよ。
平成15年11月24日
![]()
![]() は、
は、![]() の元と、
の元と、![]() とを
加減乗除によってうまく組み合わせて作ったものの全体のなす環」
と考えればよい。
後者の場合には、具体的に
とを
加減乗除によってうまく組み合わせて作ったものの全体のなす環」
と考えればよい。
後者の場合には、具体的に ![]() を構成する必要がある。(
この場合には、
を構成する必要がある。(
この場合には、![]() の関係式を別途記述する必要があるため、
の関係式を別途記述する必要があるため、
![]() という記号だけでは
通常不十分である。)
という記号だけでは
通常不十分である。)