


: この文書について...
代数学特論II 要約 No.9
今日のテーマ:

十分大きな関数空間(例えば
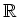 上の複素数値
上の複素数値 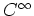 -関数の全体)を
一つ固定して、
-関数の全体)を
一つ固定して、
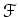 と書こう。次のような微分方程式を解きたい。
と書こう。次のような微分方程式を解きたい。
(
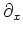 とは
とは
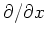 のこと。以下同様)
この方程式は
のこと。以下同様)
この方程式は
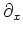 という
という
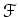 上の線型作用素が、
解の空間
上の線型作用素が、
解の空間 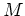 上満たす関係式と考えることができる。
上満たす関係式と考えることができる。
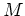 は実際は
は実際は
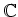 上有限次元であって、今までの線型代数の知識を
活用することができる。
上有限次元であって、今までの線型代数の知識を
活用することができる。
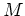 には
には
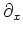 が作用していて、
が作用していて、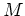 は
は
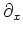 の
の 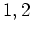 という二つの
固有値により固有分解される。
という二つの
固有値により固有分解される。
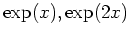 が固有ベクトルである。
が固有ベクトルである。
同様に
についても線型代数的な解釈ができる。
今度は解空間上
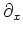 の固有値が重複して出てくるところに注意が必要である。
の固有値が重複して出てくるところに注意が必要である。
高階の方程式、例えば
でも事情は同じである。
平成15年12月1日
![]()
![]() 上の複素数値
上の複素数値 ![]() -関数の全体)を
一つ固定して、
-関数の全体)を
一つ固定して、
![]() と書こう。次のような微分方程式を解きたい。
と書こう。次のような微分方程式を解きたい。
![]() には
には
![]() が作用していて、
が作用していて、![]() は
は
![]() の
の ![]() という二つの
固有値により固有分解される。
という二つの
固有値により固有分解される。