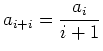![]()
先週は、「十分大きな関数空間」
![]() を考えると言ったが、
これでは大きすぎるということもあるし、もっと具体的な形が知りたいこともある。
そこで、次のような空間を用意しよう。
を考えると言ったが、
これでは大きすぎるということもあるし、もっと具体的な形が知りたいこともある。
そこで、次のような空間を用意しよう。
![$\displaystyle {\mathbb{C}}[[x]]=\{
\sum_{i=0}^\infty a_i x^i ; a_i \in {\mathbb{C}}
\}
$](img3.png)
但し、この講義では専ら
![]() の
の
![]() -ベクトル空間としての
構造に注目し、積に着目することは少ない。
-ベクトル空間としての
構造に注目し、積に着目することは少ない。
さらに、
![]() 上には
上には ![]() 倍と
倍と
![]() がともに作用している。
がともに作用している。
![]() の元は
の元は
![]() の無限和であり、
したがって
の無限和であり、
したがって
![]() は
は
![]() の
「基底」に近い扱いをすることができる。(正確には、「基底」という場合には
どんな元も有限和で書けなければならないので、ここで言うのは「位相ベクトル空間
としての基底」と呼ばれるものである。)
の
「基底」に近い扱いをすることができる。(正確には、「基底」という場合には
どんな元も有限和で書けなければならないので、ここで言うのは「位相ベクトル空間
としての基底」と呼ばれるものである。)
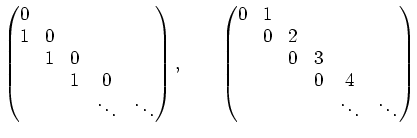
線型常微分方程式を解くとは、 この二つの行列やそれらを組み合わせてできる行列の 核の性質を調べていることだともいえる。 これら二つの行列は可換でないことにも注意しておこう。
形式的べき級数環の元の範囲で微分方程式を求めるには、係数を
イモヅル式に求めていくのが有効である場合が多い。
例えば、
![]() なる
なる
![]() を求めるには、
を求めるには、
![]() と書いて、
と書いて、