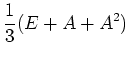: この文書について...
要約 No.1
今日のテーマ:

- いろいろな群を行列を使って具体的に表示する。(表現)
- どのような表現が可能か。
- それらの表現をどのようにして得るか。
- 群や、その表現を詳しく調べる。
例えば、
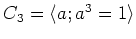 は、3乗して単位元になるような元
は、3乗して単位元になるような元 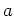 によって生成される群である。
によって生成される群である。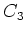 は 3つの元
は 3つの元 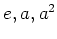 からなる。
行列で、
からなる。
行列で、
と書いてみると、
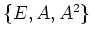 は
は 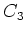 の具体的な表現を与えていることが分かる。
3次の対称群
の具体的な表現を与えていることが分かる。
3次の対称群 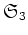 も、上の
も、上の 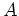 と、
で生成される群として具体的に記述することができる。
と、
で生成される群として具体的に記述することができる。
問題 1.1
上の行列
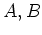
で生成された群の全ての元を成分を使って書き出しなさい。
[各回の問題はレポートで提出すること。提出は特に指定しない限り
次回の講義の終了時間に行う(土基に直接渡す)ものとする。
複数の問題がある場合には、特に指定しない限りは
各回につき一問を解けばよい。
(介護等実習など、やむを得ない場合には
その旨告げれば受け取ります。)]
上の表現は群の「置換表現」として知られるものの特別な場合である。
一般に、行列を眺めるときにはその列ベクトルに特に注目すると
よいことが多い。
例えば、基本ベクトル
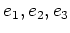 の
の 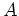 による行き先は
による行き先は
であることが分かる。
行列による表現は他にもいろいろとあり得る。 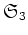 の別な表現として、
の別な表現として、
で生成されるものがある。
群にはもともと演算が一種類(かけ算)しかないのであるが、
行列表現を作った途端に、なんとなく足し算も考えてみたくなる。
例えば、はじめに述べた 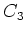 の表現で、
の表現で、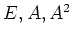 の「平均」であるところの
の「平均」であるところの
という行列を考えてみると、これは 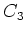 の元で動かないようなベクトル空間への
の元で動かないようなベクトル空間への
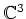 の射影を与えていることがわかる。
の射影を与えていることがわかる。
このような考えを正当化するには例えば群環というものを使うことになる。
問題 1.2
今日の講義で述べた群以外の有限群(元の数が有限個の群)の行列による表現
を一つ考えなさい。
2003/4/14
![]()
![]() は、3乗して単位元になるような元
は、3乗して単位元になるような元 ![]() によって生成される群である。
によって生成される群である。![]() は 3つの元
は 3つの元 ![]() からなる。
行列で、
からなる。
行列で、
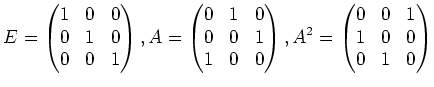
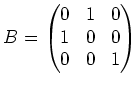
![]() の
の ![]() による行き先は
による行き先は
![]() の別な表現として、
の別な表現として、
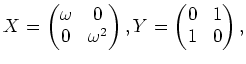
![]() の表現で、
の表現で、![]() の「平均」であるところの
の「平均」であるところの