![]()
環 ![]() と有限群
と有限群 ![]() が与えられているとき、
群環
が与えられているとき、
群環 ![]() が定義されることを前回示した。
が定義されることを前回示した。
実は、![]() は
は ![]() 自体の上に表現できる。
このことを、とくに
自体の上に表現できる。
このことを、とくに ![]() が体
が体 ![]() のときに詳しく見てみることにする。
のときに詳しく見てみることにする。
まず、群の表現の定義からしておこう。
一般に、可換体 ![]() 上の一般線型群
上の一般線型群
![]() とは、
とは、
![]() の元を成分に持つような行列で、その行列式が可逆であるようなものを
全部集めた物である。
つまり、
の元を成分に持つような行列で、その行列式が可逆であるようなものを
全部集めた物である。
つまり、

![]() 上の
上の ![]() の
の ![]() -次元表現
-次元表現 ![]() が決まると、
が決まると、
![]() の元
の元 ![]() の
の ![]() の元
の元 ![]() への「作用」が
への「作用」が
逆に、このような「作用」があれば、上の定義の意味での表現を 定義することができる。行列を書くよりもその方が簡明であることが多いので、 以下では多くの場合作用でもって表現を定義する。
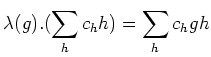
厳密にいえば、![]() の元にどのように順番を付けるかによって
の元にどのように順番を付けるかによって
![]() の各元を表す行列は違ってくる。
このことについてはもっと後で詳しく調べるが、さしあたっては、
の各元を表す行列は違ってくる。
このことについてはもっと後で詳しく調べるが、さしあたっては、
![]() の元の順番は適当に付けて、それを明示した上で行列で表現する
ことにする。
の元の順番は適当に付けて、それを明示した上で行列で表現する
ことにする。