


: この文書について...
代数学II要約 No.5
今日のテーマ:
![\fbox{
\begin{minipage}{10cm}
同型な表現(基底の変換)。\\
群 $G$\ の表現と群環 $K[G]$-加群が同じものであること。
\end{minipage}}](img1.png)
群の表現は 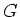 から
から
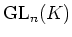 への群準同型として定義されたが、
それは
への群準同型として定義されたが、
それは 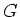 の
の 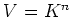 への「作用」としても決めることができたことを
思い出そう(No.3).
への「作用」としても決めることができたことを
思い出そう(No.3).
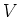 のことを
のことを
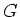 の作用をこめて
の作用をこめて
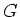 -加群とよぶことがある。
-加群とよぶことがある。
定義 5.1
群
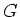
が
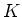
上の二つのベクトル空間
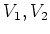
に作用しているとする。
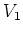
から
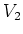
への全単射
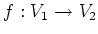
があって、
次の条件をみたすとき、
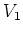
と
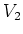
は
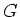
の作用をこめて同型
(
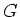
-加群として同型)であるという。
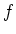 は
は 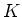 -ベクトル空間としての準同型である。
つまり、足し算、スカラー倍を保つ。
-ベクトル空間としての準同型である。
つまり、足し算、スカラー倍を保つ。
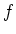 は
は  の作用を保つ。
の作用を保つ。
補題 5.1
群準同型
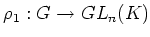
と
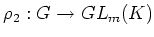
から
きまる
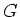
-加群
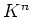
と
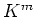
が
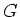
-加群として同型である
ための必要十分条件はある正則行列
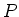
があって、
任意の
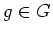
に対して、
が成り立つことである。
(このような 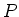 が存在するとき、
が存在するとき、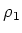 と
と 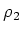 とは同値であるといわれる。
とは同値であるといわれる。
とくに、同じベクトル空間の基底をいろいろ取り換えても
同値な表現が得られる。
同値な表現同士はある意味で「同じ」ものであるが、どうせ同じものを
見るのならば基底をうまくとって表現行列が簡単になるようにしたほうがよい。
ついでに、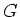 -加群と
-加群と ![$ K[G]$](img23.png) 加群は同じものの違う見方であることを
述べておこう。
加群は同じものの違う見方であることを
述べておこう。
定義 5.2
一般に、環
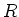
に対して、
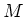
が
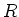
-加群であるとは、
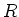
の
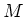
への「作用」
が決まっていて、次の条件を満たす時にいう。
-
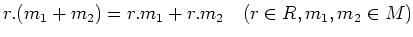
-
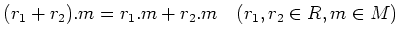
-
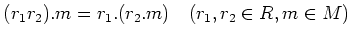
-
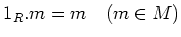
補題 5.2
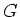
-加群
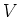
は、自然に
![$ K[G]$](img23.png)
-加群とみなせる。
その逆も正しい。
問題 5.1
位数
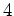
の巡回群
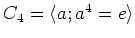
の正則表現
で
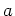
に対応する行列
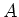
をもとめ、さらに正則行列
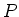
をうまくとって
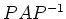
をできるだけ簡単な行列で表現せよ。
平成15年5月19日
![\fbox{
\begin{minipage}{10cm}
同型な表現(基底の変換)。\\
群 $G$\ の表現と群環 $K[G]$-加群が同じものであること。
\end{minipage}}](img1.png)
![\fbox{
\begin{minipage}{10cm}
同型な表現(基底の変換)。\\
群 $G$\ の表現と群環 $K[G]$-加群が同じものであること。
\end{minipage}}](img1.png)
![]() から
から
![]() への群準同型として定義されたが、
それは
への群準同型として定義されたが、
それは ![]() の
の ![]() への「作用」としても決めることができたことを
思い出そう(No.3).
への「作用」としても決めることができたことを
思い出そう(No.3).
![]() のことを
のことを
![]() の作用をこめて
の作用をこめて
![]() -加群とよぶことがある。
-加群とよぶことがある。
![]() -加群と
-加群と ![]() 加群は同じものの違う見方であることを
述べておこう。
加群は同じものの違う見方であることを
述べておこう。