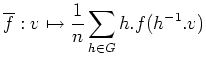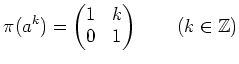: この文書について...
代数学II要約 No.6
今日のテーマ:

以下、とくに断らない限り、群といえば有限群、ベクトル空間や表現といえば
有限次元のものをさすことにする。
前回も少し述べたように、次のものは実質的に同じものになる。
 の表現
の表現
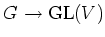
- 体
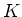 上のベクトル空間
上のベクトル空間 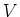 で、その上に
で、その上に  の作用が定まったもの
(
の作用が定まったもの
(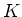 上の
上の  -加群)
-加群)
- 環
![$ K[G]$](img6.png) 上の加群
上の加群
これらのどの言葉を選ぶかによって、以下の説明の言葉遣いも変わってくる
のだが、さしあたっては 《 -加群》という言葉遣いを主に使うことにする。
(この講義のもう少し後では環論的な立場を重視するために、
-加群》という言葉遣いを主に使うことにする。
(この講義のもう少し後では環論的な立場を重視するために、![$ K[G]$](img6.png) -加群
の言葉を使うことになる。)
-加群
の言葉を使うことになる。)
定義 6.1
群

と、体
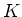
上の

-加群
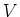
が与えられているとする。
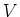
の
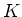
-部分ベクトル空間
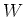
が、

-の作用で閉じている、すなわち、
が成り立つとき、
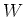
はそれ自身

-加群になる。このような
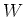
のことを
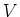
の

-部分加群とよぶ。
補題 6.1
体
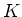
上の

-加群
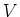
と、その部分加群
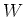
とが与えられているとき、
剰余ベクトル空間
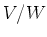
も 自然に

-加群の構造をもつ。
(
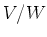
のことを
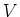
の
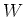
による剰余

-加群とよぶ。)
定義 6.2
体
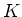
上の

-加群
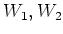
があるとき、直和ベクトル空間
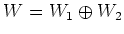
には自然に

-加群の構造が入る。(
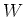
を

-加群
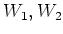
の直和という。)
定理 6.1 (マシュケの定理)
有限群

の元
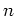
が、体
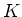
の中で 0 と異なるとき、
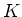
上の

-加群
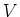
とその

-部分加群
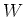
とに対して、
ある
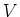
の部分加群
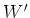
が存在して、
がなりたつ。
マシュケの定理の証明には次の補題が鍵になる。
補題 6.2 (線型写像の「平均」)
有限群

の元
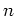
が、体
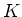
の中で 0 と異なるとする。
体
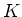
上の

-加群
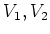
と、
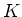
-線型写像
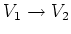
があるとする。このとき、
によって定まる
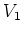
から
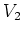
への
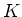
-線型写像
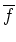
は、

-加群としての
準同型になっている。すなわち、
が任意の
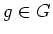
に対してなりたつ。
問題 6.1
位数
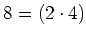
の二面体群(正方形の合同変換群)
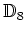
は
で生成される
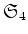
の部分群と同一視される。
この群
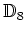
の置換表現(
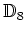
の
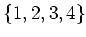
への
作用から定まる4次元表現)を二つ(以上)の表現の直和に分解せよ。
問題 6.2 (お詫びと訂正:この問題は間違いでした。すみません)
写像の平均は写像の合成と可換であることを示せ。すなわち、
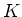
-上の

-加群
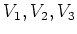
があって、
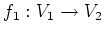
,
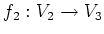
なる
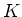
-線型写像が
与えられているとき、
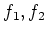
に対して補題のように「平均」
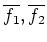
を定めると、
が成り立つことを示しなさい。
ただし、

の位数
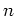
は
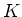
で 0 ではないとする。
問題 6.3 (マシュケの定理の最初の条件はなぜ必要か)
素数
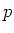
が与えられたとき、
は元の個数が
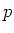
の体になる。
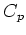
の
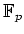
上の 2次元表現を、
によって定めると、
この表現は一次元部分表現をもつにもかかわらず、
いかなる一次元表現二つの直和にも書き表すことができないこと、
すなわち
この表現はマシュケの定理の後半を満たさないことを示しなさい。



: この文書について...
2003/6/11
![]()
![]() -加群》という言葉遣いを主に使うことにする。
(この講義のもう少し後では環論的な立場を重視するために、
-加群》という言葉遣いを主に使うことにする。
(この講義のもう少し後では環論的な立場を重視するために、![]() -加群
の言葉を使うことになる。)
-加群
の言葉を使うことになる。)